Question

What does discontinuity mean in math?

Answer 1

A function has a discontinuity if it isn't well-defined for a particular value (or values); there are 3 types of discontinuity: infinite, point, and jump.

Many common functions have one or several discontinuities. For instance, the function `y=1/x` is not well-defined for `x=0`, so we say that it has a discontinuity for that value of `x`. See graph below.

Notice that there the curve does not cross at `x=0`. In other words, the function `y=1/x` has no y-value for `x=0`.

In a similar way, the periodic function `y=tanx` has discontinuities at `x=pi/2, (3pi)/2, (5pi)/2...`

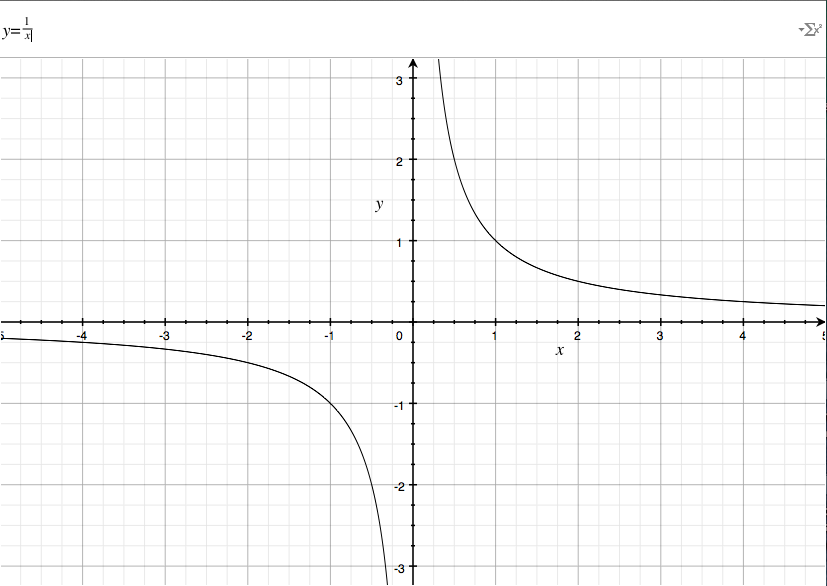Infinite discontinuities occur in rational functions when the denominator equals 0. `y=tan x=(sin x)/(cos x)`, so the discontinuities occur where `cos x=0`.

Point discontinuities occur where when you find a common factor between the numerator and denominator. For example,
`y=((x-3)(x+2))/(x-3)`
has a point discontinuity at `x=3`.

Point discontinuities also occur when you create a piecewise function to remove a point. For example:
`f(x)={x, x!=2; 3, x=0}`
has a point discontinuity at `x=0`.

Jump discontinuities occur with piecewise or special functions. Examples are floor, ceiling, and fractional part.