Question

How do I find the value of `log 1000`?

Answer 1

The answer is 3.

You can do this in 2 different ways.

One is to just plug it in your calculator, and the other is by hand.

By hand, you need to know that `log` is the same thing as `log_10`.

Therefore, if you rewrite the problem as such, you get:

`log_10 1000` = ?

From here, it would be a lot easier to solve this problem by converting the logarithm into exponential form (which is simply something with an exponent, like `5^2`)

To understand how to do this, refer to the image below:


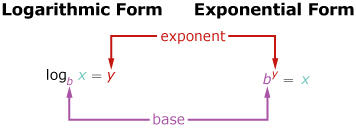
So therefore we can rewrite the problem as:

`10^? = 1000`

And if you know your exponents right, you'll know that `10^3=1000`

Hence, the answer is 3.

To know more about how logarithms work, please refer to my explanation in this other answer I contributed to.

Hope that helps :)

Answer 2

`log_10 1000 = 3`

Explanation:

Think of an expression given in log form as asking a question.
Logs are very closely linked to indices (powers).

(If no base is given, it is always 10.)

In `log_10 1000` The question being asked is..

"What index (power) of `10 " will make " 1000?`"

OR

`"How can I make " 10 " into " 1000 " using an index (power)?"`

You should know that our number system is based on.

`10^1 = 10`
`10^2 = 100`
`10^3 = 1,000` and so on.

So we can say that "10 raised to the power of 3 is 1000"

Using this to answer the log question gives:

`log_10 1000 = 3`

In the same way: `log_3 9 = 2 " "rarr` because `3^2 = 9`

Can you explain why the following are true?

`log_5 25 = 2color(white)(xxxx)log_4 64 = 3color(white)(xxxx)log_9 81 = 2`

`log_10 10 = 1color(white)(xxxx)log_5 625 = 4color(white)(xxxx)log_10 1 = 0`