How do you find the horizontal asymptote of the graph of y=3x^6-7x+10/8x^5+9x+10?
1 Answer
Unfortunately,
does not have any horizontal asymptote; however, it has a slant asymptote
Its graph looks like this:
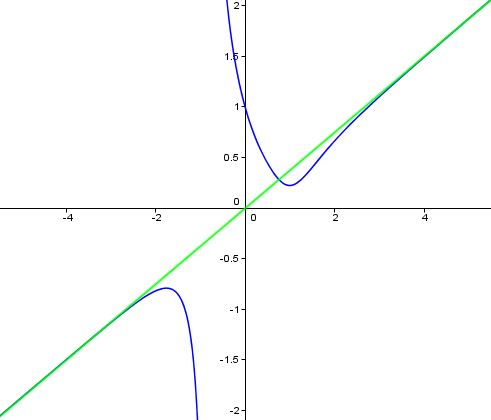
Let us look at some details.
by dividing by
Since the limits at infinity do not exist, there are no horizontal asymptotes.


