Question

`sf(""^24Na)` undergoes `beta` decay. A 208g sample decays such that 13g remain. What is the 1/2 life ?

Answer 1

If we begin with 208 grams at the end of 1 half-life there would be 104 grams remaining, at the end of the 2nd half-life there would be 52 grams, at the end of the 3rd half-life there would be 26 grams and at the end of the 4th half-life there would be 13 grams.

The total time of decay is 60 hours and this represents 4 half-lifes.

#(60 hours)/(4 half-lifes) = 15 hours/half-life

The half-life for Sodium-24 is 15 hours.

Answer 2

The above answer is a good answer for that specific question so I will give an answer for a more general situation where the numbers may not work out so nicely.

For a random event such as the decay of a radioactive nucleus the rate of decay depends only on the number of undecayed atoms.

`RatepropN`

We replace the proportional sign by a constant , in this case the Greek letter lambda `lambda`.

Since the number of atoms is decreasing we can write:

`Rate=-lambdaN`

`lambda` is called the decay constant and is a measure of how quickly the isotope is decaying.

You may have seen the same thing if you have studied 1st order reaction kinetics - the theory is just the same and applies to many natural processes referred to as "exponential decay". `lambda` is directly analogous to the rate constant k in chemical kinetics.

A typical decay curve looks like this:

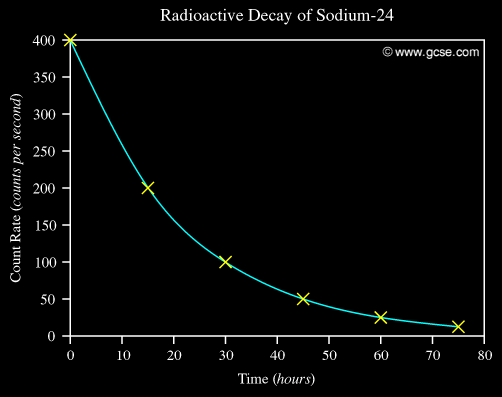
By doing some mathematics using integration (which I won't go into here) we get:

`N_t=N_0e^(-lambdat)`

`N_t` are the number of undecayed atoms at time t
`N_0` are the initial number of atoms
`lambda` is the decay constant which I described earlier
`t` is the time elapsed.

To turn this expression into a more usable form we take natural logs of both sides to give:

`lnN_t=lnN_0-lambdat`

So

`lnN_t-lnN_0=-lambdat`

`rArr`

`ln((N_t)/(N_0))=-lambdat`

We can use mass in grams for numbers of atoms (since they are proportional) so we can put in the numbers to get `lambda`:

`ln((13)/(208))=-lambda*60`

`-2.77=-lambda*60`

`lambda = 0.046 s^(-1)`

The faster the decay (related to `lambda`), the shorter the half - life. The relation between the two is given by this expression (again I won't bother you with the derivation):

`t_(1/2)=0.693/lambda`

So:

`t_(1/2)=0.693/0.046=15s`

So you can use a particular value of `N_t` and `N_0` to get `lambda` and hence `t_(1/2)`.