Using the unit circle, how do you find the value of the trigonometric function: sec(-227pi/4) ?
1 Answer
Sep 17, 2015
Explanation:
First let's work that value within the secant to reveal the biggest integer amount of
The period of the secant is
The secant is an even function, that is,
So,
Now, we can either just look at the unit circle or continue using formulas. Since you specifically asked for the unit circle, we should look for
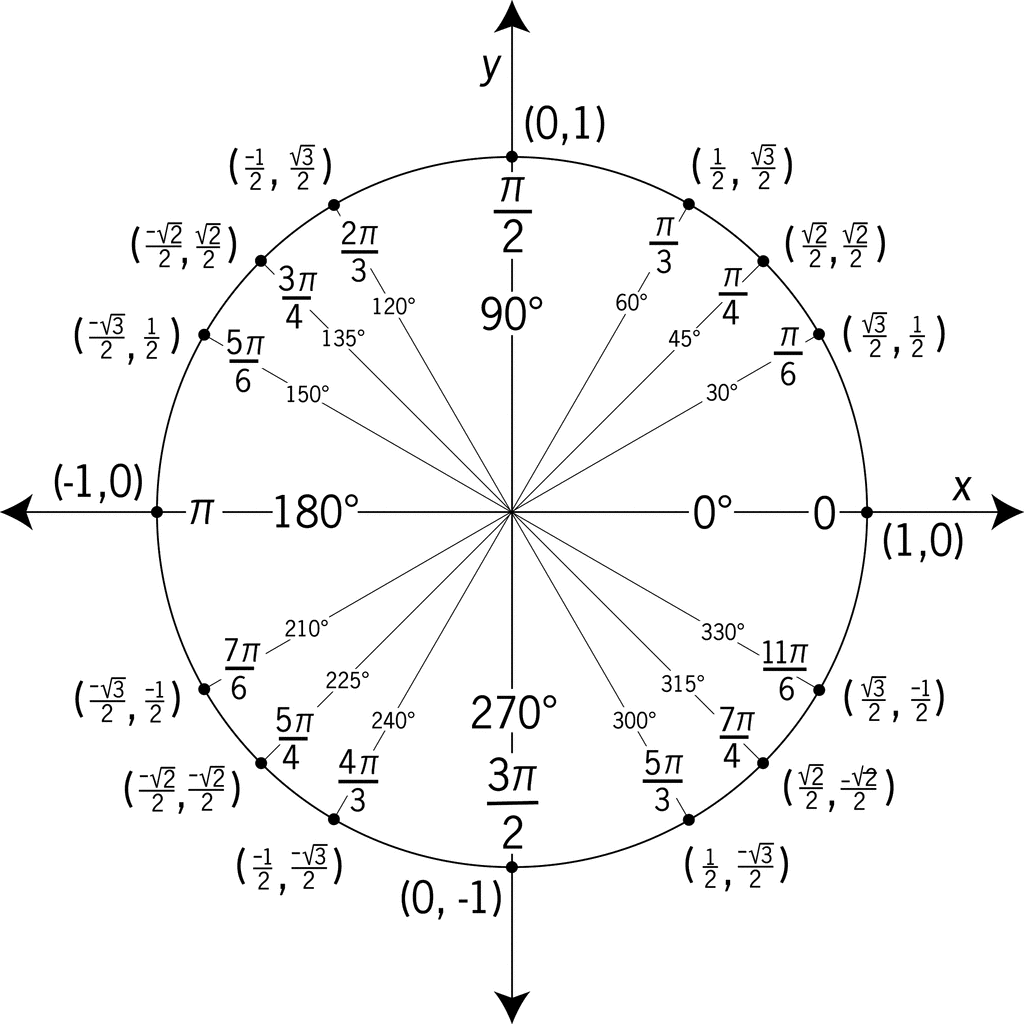
We see that
So,

