So, when we have a quadratic equation:
ax2+bx+c=0
One of the ways we can solve for x is by using the quadratic formula:
)
But wait... for your problem, there's no x! Taking a look at the equation, the first thing we need to do is realize that x is just a placeholder for any variable (a number that we don't know... yet). In your question, the variable is shown as m. It's the same thing; we could call it x or m or ω or whatever we like.
Now, we need to figure out the values of a, b, and c. a is the number before the x2 variable (or, in your case, m2). b is the number before m, and c is the number not associated with the variable. So...
a=5
b=−11 (don't forget that negative sign!)
c=−3 (again, the negative sign is important)
Now, we can take those three numbers and plug them into the quadratic equation:
x=⎛⎜
⎜⎝−(−11)(±)√(−112)−(4)(5)(−3)(2)(5)⎞⎟
⎟⎠
See that ± in there? That means we're going to get two answers.
Either
x=⎛⎜
⎜⎝−(−11)(+)√(−112)−(4)(5)(−3)(2)(5)⎞⎟
⎟⎠
OR
x=⎛⎜
⎜⎝−(−11)(−)√(−112)−(4)(5)(−3)(2)(5)⎞⎟
⎟⎠
x can either be 2.445 or -0.2453 (leaving off quite a few decimal places)
Let's check to make sure that's right, by plugging in our values for x:
Does (5)(2.4452)+(−11)(2.445)+(−3)=0?
Does (5)(0.24532)+(−11)(0.2453)+(−3)=0?
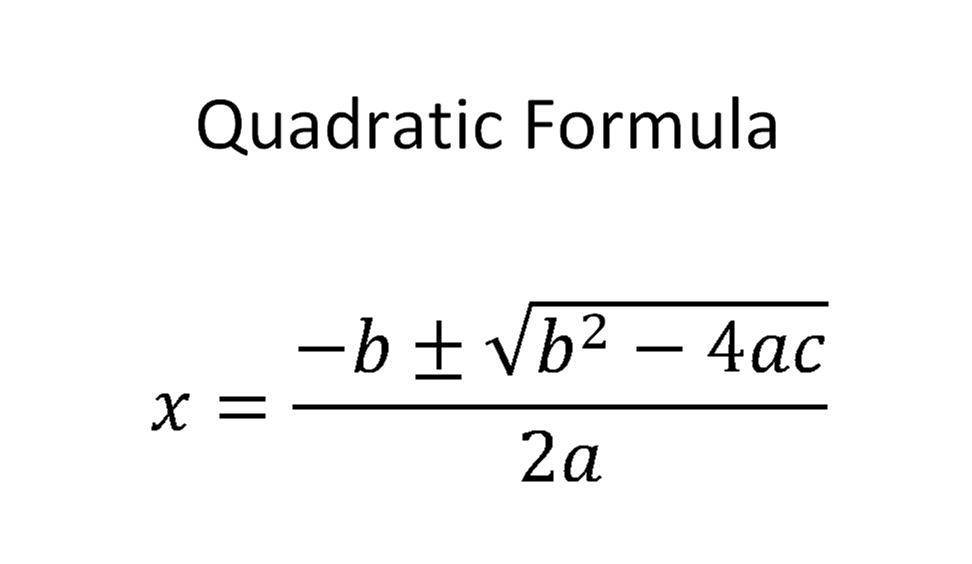