To solve this, we need to know the values of the #sin# and #cos# functions at specific angles. One of the simplest ways to look at this is using the unit circle. If we plot a point on the circle that makes the angle #theta# with the positive #x# axis in the counter clockwise direction, then the value of #cos(theta)# is the projection from that point onto the #x# axis, and the value of #sin(theta)# is the projection from that point onto the #y# axis.
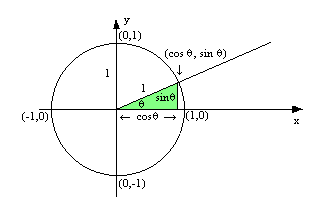
Starting with #sin^2(pi//2) = (sin(pi//2))^2# we need to know the #sin# of the angle #theta = pi//2#. This is a #90^o# angle putting us at the point #(0,1)# on the unit circle. Therefore, the #sin# of this angle is #1#.
#sin^2(pi//2) = 1^2 = 1#
The next term is #cos(pi)#. This is an angle of #180^o# which puts us at the point #(-1,0)# on the unit circle, which means that the #cos# of this angle is #-1#
#cos(pi) = -1#
Now we need to put them together:
#sin^2(pi//2)-cos(pi) = 1 - (-1) = 2#

