How do you integrate $int x^3e^x$ by integration by parts method?

Question

10664 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-02T11:59:54

Using integration by parts: $=e^x ( x^3 - 3x^2 + 6x - 6)+C$

The equation for integration by parts is this:

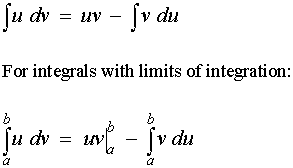
$math.info$ math.info

I think mathematicians use similar letters on purpose to confuse people. Thats why they chose $u$ and $v$ , the worst possible letters.

Anyways, we have to pick our $u$ .

let $u = x^3$ so $du = 3x^2dx$

That leaves the rest of the integral to be $dv$

let $dv = e^xdx$ so by taking the integral of both sides, $v = e^x$

To recap, so far, we have

so $int u dv = uv - int v du$
$=x^3*e^x - inte^x*3x^2dx$

So lets go again!

$x^3*e^x - inte^x*3x^2dx$
$= x^3*e^x - (3x^2*e^x - inte^x*6xdx)$

So lets go again (because calculus is so fun)!

$= x^3*e^x - (3x^2*e^x - inte^x*6xdx)$
$= x^3*e^x - (3x^2*e^x - (6x*e^x - int e^x*6dx))$

Simplify

$= x^3*e^x - (3x^2*e^x - (6x*e^x - 6e^x))$
$= x^3*e^x - (3x^2*e^x - 6x*e^x + 6e^x)$
$= x^3*e^x - 3x^2*e^x + 6x*e^x - 6e^x$

Then you can take out the $e^x$ term if you'd like

$=e^x ( x^3 - 3x^2 + 6x - 6)$

Don't forget to add + C at the end, to signify that there is a group of equations what this integral could be.

$=e^x ( x^3 - 3x^2 + 6x - 6)+C$

How do you integrate int x^3e^xint x^3e^x by integration by parts method?