Although this question is marked as a Trigonometry question, the solution requires calculus to solve.
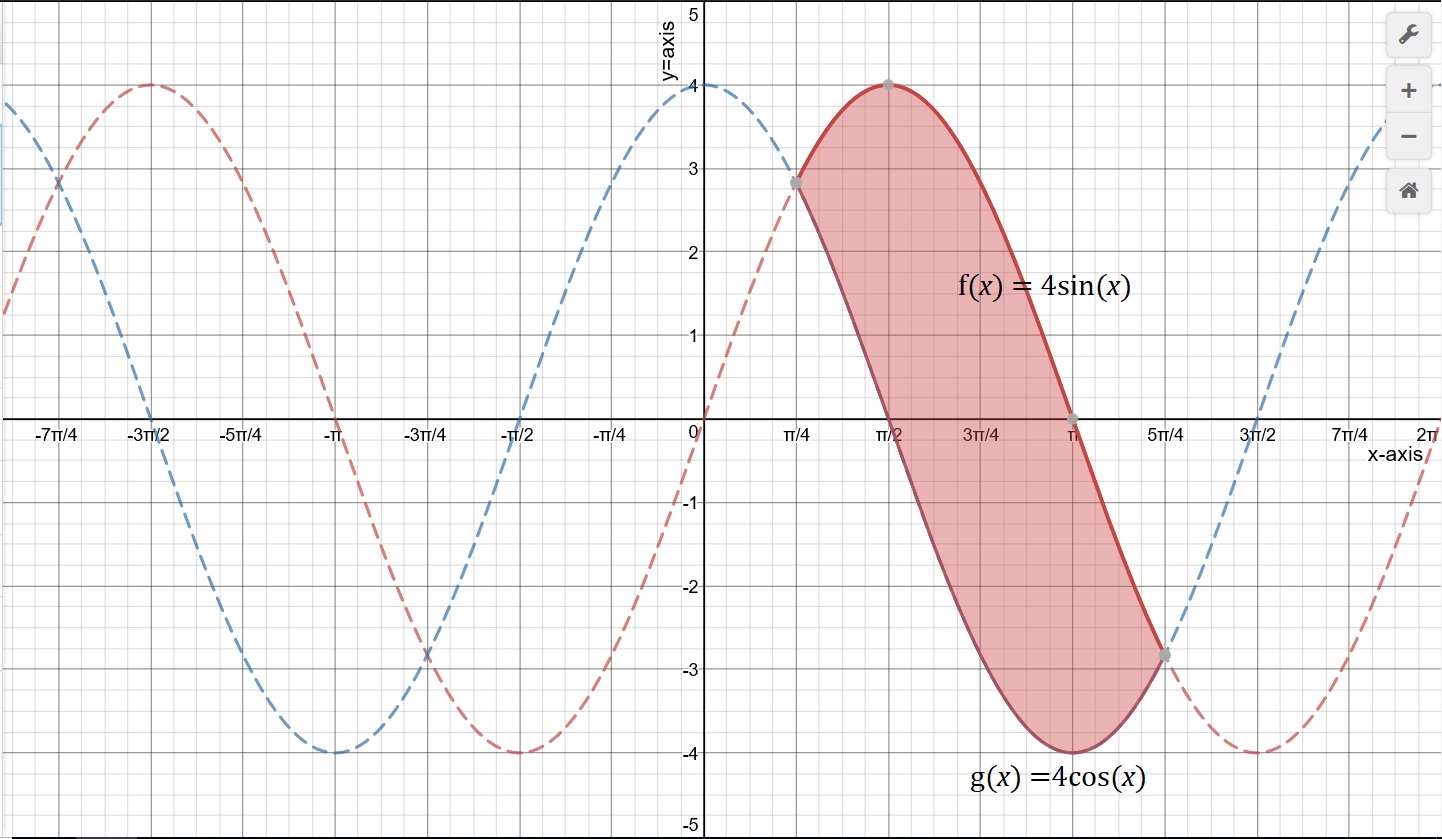
You are given two curves and want to find the space between them, as depicted by this graph.
Let #f(x) = 4sin(x)#.
Let #g(x)=4cos(x)#.
 )
)
The #x#-coordinate of the left hand side intersection is #a=pi/4#.
The #x#-coordinate of the right hand side intersection is #b=(5pi)/4#.
The positive area above the #x#-axis is equal to the negative area below the #x#-axis and would cancel each other out. So we must stick to finding the area above the #x#-axis and then double that area.
One strategy would be to find the area, #A# under #f(x)=4sin(x)# between #x=pi/4# and #x=pi# and then subtract off the area, #B#, of #g(x)=4cos(x)# between #x=pi/4# and #x=pi/2#. Finally, we would need to double that area to find the total area, #A_"Total"#, both above and below the #x#-axis. In other words, we are finding #2(A-B).#
Area #A# is
#A=int_(pi/4)^pi4sin(x)dx=[-4cos(x)]_(pi/4)^pi#
#= 4+2sqrt(2)#
Area #B# is
#B=int_(pi/4)^(pi/2)4cos(x)dx=[4sin(x)]_(pi/4)^(pi/2)#
#B=4-2sqrt(2)#
Therefore, the total area #A_"Total"# is
#A_"Total"=2(A-B)#
#" "=2(4+2sqrt(2)-4+2sqrt(2))#
#" "=8sqrt(2)~~11.31#
 )
) 