#cot765^@ = #? #sec765^@ = #? #csc765^@ = #?
2 Answers
Dec 1, 2017
Explanation:
#"note that "765^@=765-720^@=45^@#
#rArrcot765^@=1/(tan45^@)=1/1=1#
#rArrsec765^@=1/(cos45^@)=1/(1/sqrt2)=sqrt2#
#rArrcsc765^@=1/(sin45^@)=1/(1/sqrt2)=sqrt2#
Dec 1, 2017
Explanation:
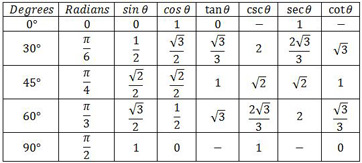
Since, they are all in the same quadrant,
With the help of this chart, we can, hence, easily solve the equation.