In a limit, what is the difference between #lim_(x->a)#, #lim_(x->a^-)#, #lim_(x->a^+)# where #ainRR#?

2 Answers
SoySoy4444
Dec 11, 2017

#lim_(xrarra^-)# and #lim_(xrarra^+ )# is an one-sided limit.
#lim_(xrarra)# is from both directions- left and right.
#lim_(xrarra^-)#is only from the left hand side.
#lim_(xrarra^+)#is only from the right hand side.

Explanation:

#lim_(xrarra^-)# and #lim_(xrarra^+ )# is an one-sided limit..
This means it approaches a certain value from only one side.

#lim_(xrarra)# is from both directions: left and right.
#lim_(xrarra^-)#is only from the left hand side.
#lim_(xrarra^+)#is only from the right hand side.

Example

#(x^2+1)/x#
graph{(x^2+1)/x [-10, 10, -5, 5]}
#lim_(xrarr1)# would be #2# because near #x=1#, it is approaching #2# from BOTH sides.

#lim_(xrarr0^+)# would be #oo# because near #x=0#, it is approaching #oo# from the RIGHT side.

#lim_(xrarr0^-)# would be #-oo# because near #x=0#, it is approaching #-oo# from theLEFT side.

On the other hand, #lim_(xrarr0)# DOES NOT EXIST because there has to be a certain number it approaches at #x=0# from BOTH sides.

Steve M
Dec 11, 2017

#lim_(x rarr a^-)# denote the left sided limit, we are interested in the behaviour as we approach the function from the LHS

#lim_(x rarr a^+)# denote the right sided limit, we are interested in the behaviour as we approach the function from the RHS

#lim_(x rarr a)# denote the limit irrespective of the direction approach and only exists if the LHS limit and the RHS limit are identical. The limit can (but does not need to be) the value of the function at #a#

Consider a Function:

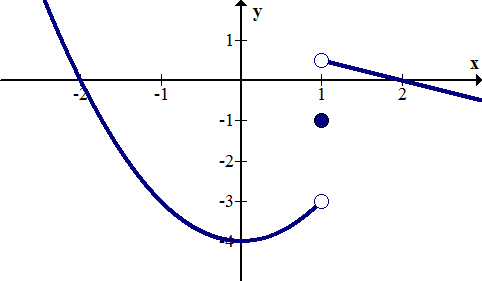
https://www.ck12.org/book/CK-12-Precalculus-Concepts/section/1.10/

Here, # f(x) = { (x^2-4, x lt 1), (-1, x = 1), (-1/2x+1, x gt 1 ) :} #

Then consider the limits as we approach #x=1#

For #lim_(x rarr a^- \ )f(a)# we consider points to the left of #x=1#, the definition describes these points as being on the quadratic portion, no matter how close we get to #x=1# we never leave the quadratic portion: thus:

#lim_(x rarr a^- \ )f(a)=-3#,

Similarly #lim_(x rarr a^+ \ )f(a)# we consider points to the right of #x=1#, the definition describes these points as being on the linear portion, no matter how close we get to #x=1# we never leave the linear portion: thus:

#lim_(x rarr a^+ \ )f(a)=1/2#,

Even though #f(1)# is defined and #f(1)=-1#, the limit

# lim_(x rarr a \ )f(a)#

does not exist as the LHS limit does not equal the RHS limit.

The last point is critical as it shows that the value of the limit at any particular point does not necessarily have to be the same as the value of the function at the point. If the two are the same the function is said to be "continuous" at that point; otherwise it is "discontinuous" (as in this example)

Related questions
Impact of this question
4135 views around the world
You can reuse this answer
Creative Commons License