A few ways of approximating the bell curve...
The general Bell curve:
#color(red)(y = 1/sqrt(2pi) e^(-1/2 x^2 )#
 )
)
There are many reasons to why you may want to approximate the bell curve, one being that it is particulaly difficult to integrate definitely...
So by approximating, and finding a function that is more easy to integrate definitely, and has an antiderivative, this is much eaiser.
The first thing I can think of is utilising a function that already has #e^x# within it, then we consider #color(blue)(coshx -= 1/2 ( e^x + e^-x ) #
But by sketching, this doesnt quite have the general shape, so the reciprical could be a good idea:
#color(orange)(sech x -=1/coshx -= 2/(e^x+e^(-x) ) #
![enter image source here]()
Now this looks more like it...
One main property of the bell curve, used in statistics regulaly...
#color(blue)(int_-oo ^ oo 1/sqrt(2pi) e^(-1/2 x^2 ) # #color(blue)(dx=1 #
This can be proven using polar substitution using the jacobian, a higher level of mathematics....
So one thing we could do, is understand what the total area under #y = sechx # is?
Finding: #int_ -oo ^oo sechx # # dx #
We can use the substitution #u = tanhx #
#=> du = sech^2 x dx #
#=> (du)/(sechx) = sechx dx #
So #int sechx dx => int (du)/sechx #
Now use #color(red)(1-tanh^2 x -= sech^2 x #
#=> sechx = sqrt(1-tanh^2 x ) #
#=> sechx = sqrt(1-u^2 ) #
#int (du)/sechx = int (du)/sqrt(1-u^2) #
Now we can use another trig substitution:
#u = sintheta #
#=> du = costheta d theta #
# int (du)/sqrt(1-u^2)#
#=> int (costheta d theta )/ (sqrt(1-sin^2 theta) )#
#=> int (costheta d theta ) / costheta #
#=> int d theta #
# = theta +c #
Using our substitutions...
#= sin^(-1) u + c #
#color(blue)(= sin^(-1) (tanhx ) + c #
Integrating indefinitely...
#[sin^(-1) (tanhx) ]_ -oo ^ oo #
#=> sin^(-1) ( tanh (oo) ) - sin^(-1)( tanh(-oo) )#
#=> sin^(-1) (1) - sin^(-1) (-1) #
#=> pi/2 - (-pi/2) #
#=> color(red)(int_-oo ^oo sechx dx = pi #
#=> color(red)(int_-oo ^oo 1/pi sechx dx = 1 #
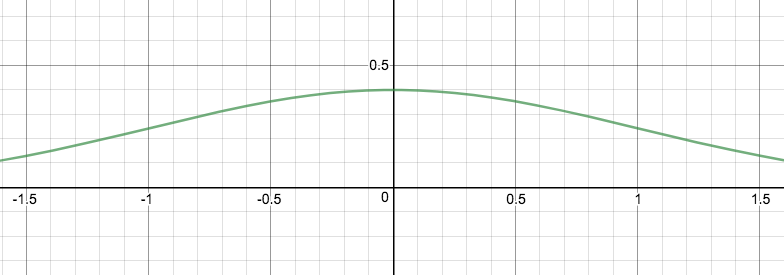
So #color(blue)(y = 1/pi sechx # is a half decent approximation for the bell curve...
![enter image source here]()
But as from looking from the graph we see that for small values of #x# this may not be the most accurate approximation
So #color(blue)(y = 1/sqrt(2pi) sechx # is a good aprpimation for small #x#:
As it has same value for #x=0# And for #x# being small
![enter image source here]()
 )
)

