How do you solve cos(2x)cos(x)+sin(2x)sin(x)=1 for all solutions?
2 Answers
See below...
Explanation:
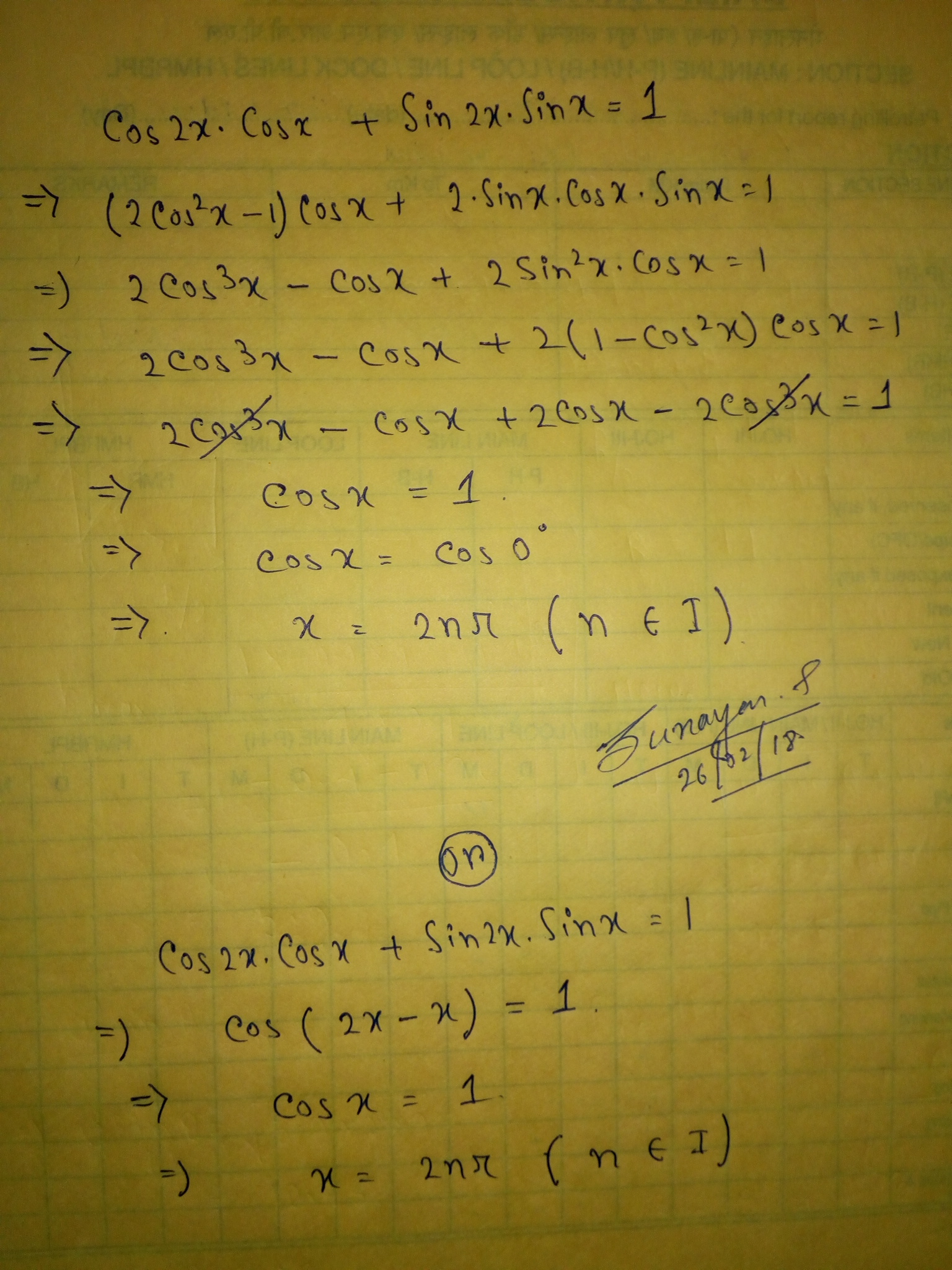
For further problem, notify me.
Apply appropriate trig identities and simplify, resulting in having to solve the equation
Explanation:
First, we want everything in this equation to be in the form of one trigonometric function. Let's have everything in the form of
Recall the following identity:
Rewrite with this applied:
Recall that
Solving for
Apply this to the instance of
Distribute
Recall the following identity:
Apply:
Multiply
Now, we have a very simple equation to solve:
We want all values of


