Question

An object falls freely from rest near the surface of earth. What is the speed of the object when it has fallen 4.9 meters from its rest position ?

Answer 1

`9.8 m/s`

Explanation:

Listed below are the four kinematic equations. Keep in mind that the kinematic equations are the same for the x-direction and y-direction for one-dimensional motion, except that the variable x is replaced with the variable y, in the equations:

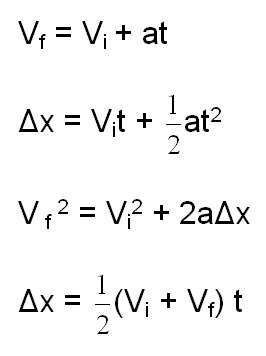
We're going to call the downwards direction the positive y-direction, which means as the object falls down, it's position is increasing in the y-direction

The quantities we know are:
- Acceleration, `a` = `+g` = `9.8 m/s^2`, because the object is falling downwards, and acceleration caused by gravity causes the object's speed to increase
- Displacement `Δy`: 4.9 m
- Initial Speed `v_i`: `0 m/s`

Because we are looking for the final speed, `v_f`, and we don't know the time, choose the equation that excludes `t`, and solve for `v_f`. In this case, it would be the third equation, and we would pick the third equation, where `v_f = sqrt(v_i^2 + 2*a*Δy)`. Therefore, after plugging numbers, `v_f = 9.8 m/s` (which happens to also be the value for acceleration caused by gravity).

Hope this helps!