A ball with a mass of #350 g# is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of #16 (kg)/s^2# and was compressed by #7/4 m# when the ball was released. How high will the ball go?
3 Answers
The height reached by the ball is
Explanation:
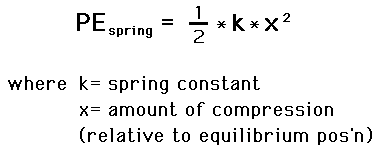
The spring constant is
The compression of the spring is
The potential energy stored in the spring is
This potential energy will be converted to kinetic energy when the spring is released and to potential energy of the ball
Let the height of the ball be
The acceleration due to gravity is
Then ,
The potential energy of the ball is
Mass of the ball is
The height reached by the ball is
First we have to find the force of the spring.
Explanation:
Using the spring constant formula this can be found
Then the acceleration is:
To find the velocity at which the ball leaves the spring the following formula can be used:
Now this is a projectile motion question.
The ball travels
Explanation:
I will assume that all of the potential energy in the spring will turn into kinetic energy and the only thing opposing the motion of the ball is the acceleration of free fall acting in the opposite direction of it's motion.
Now, the potential energy in the spring is given by:
k=spring constant
x=compression of the spring
We know that our final velocity will be 0 as this is the point where the ball will start falling down again due to the acceleration of free fall acting in the opposite direction.
Using the kinematic equation:
v=final velocity (0)
u=inital velocity
a=acceleration (-9.81, as gravity is opposing or direction of motion)
t=time
So it takes 1.193 seconds for the ball to reach its maximum height.
Now using another kinematic equation to find the distance travelled:
s=distance travlled
v=final velocity (0)
u=inital velocity- 11.71
t=time