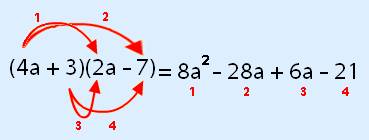Question

How do you multiply `(3x^2 + 2x + 4)(2x + 1)`?

Answer 1

`6x^3+7x^2+ 10x +4`

Explanation:

You have to take each number in the first bracket and multiply it by the second one.
First lets do `3x^2`
`(3x^2)*(2x)` and (3x^2)*1# This will give #6x^3`and`3x^2#

Then `2x`
`2x * 2x` and `2x *1`
This will give `4x^2` and `2x`

Then `4`
`4*2x` and `4*1`
This will give `8x` and `4`

Taking all these, you simply just add them together!

Answer 2

`= 6x^3 + 7x^2+10x+4`

Explanation:

Do the first term in the first bracket multiplied by the first term in the second bracket. Do the same with the first term in the first bracket (`3x^2`) and the second term of the second bracket.

(`3x^2`)x(`2x`) = `6x^3`
(`3x^2`)x(`1`) = `3x^2`

[For powers, use the rule:

`a^m`x`a^n` = `a^m+n` (where `x` is actually `x^1` from example above which simply calculates to `x`)

Then multiply any real numbers as you normally would (`3`x`2`)]

For the next step, multiply the second term of the first bracket to the first of the second bracket:

(`2x`)x(`2x`) = `4x^2`
(`2x`)x(`1`) = `2x`

Proceed to the final term in the first bracket and follow the same steps:

(`4`)x(`2x`) = `8x`
(`4`)x(`1`) = `4`

Simplify by adding all like terms together:

`= 6x^3 +3x^2+4x^2+2x+8x+4`
`= 6x^3 + 7x^2+10x+4`