Question

How do you find the domain and range of `f(x) = x^3 - 3x + 2`?

Answer 1

`D: " "(-oo, +oo)`

`R: " "(-oo, + oo)`

Explanation:

Domain simply asks, "Where does the function exist on the x-axis?" So, in this function, because `x` is cubed, it can stretch from negative infinity to positive infinity.

Similarly, range asks, "Where does the function exist on the y-axis?" When you plug the function into a graph, it becomes evident that it will forever go upward toward infinity and forever downwards toward negative infinity on both axes.

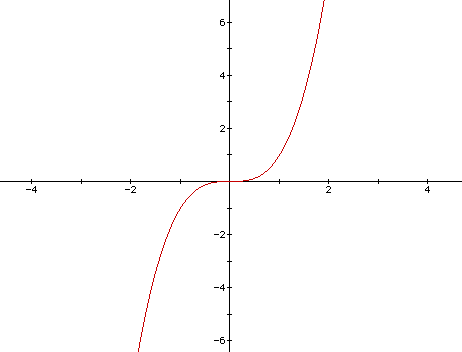This image shows the basic graph of `f(x)=x^3`.