How to find points are area with intergration?

How to do Q 12 and Q13?

enter image source here

1 Answer
Tom M.
May 13, 2018

12-#69/20#
13-
a) #A=(0,6), B=(5,5)#
b)#"area of P"=91/6#
c)#"area of Q"=125/6#

Explanation:

Q12

enter image source here

It will help us to write the equation of the curve as #y=16x^-2#

#"Area of A:"#

#"area under curve"=int_2^4(16x^-2)dx#
#=[-16x^-1]_2^4#
#=-16/4--16/2#
#-4+8#
#=4#

We can use a triangle for the area under the line, but that involves finding points of intersection, and since the line is already in the form #y="blah"#, we may as well integrate.

#"area under line"=int_2^4(1/2x-1)dx#
#=[(1/2x^2)/2-x]_2^4#
#=[1/4x^2-x]_2^4#
#=(1/4(4)^2-4)-(1/4(2)^2-2)#
#=0-(-1)#
#=1#

#:."area of A"=4-1#
#=3#

Now for B

#"area of B":#

#"area under line"=int_4^5(1/2x-1)dx#
#=[1/4x^2-x]_4^5#
#(1/4(5)^2-5)-(1/4(4)^2-4)#
#=5/4-0#
#=5/4#

#"area under curve"=int_4^5(16x^-2)dx#
#=[-16/x]_4^5#
#=(-16/5)-(-16/4)#
#=-16/5+4#
#=4/5#

#:."area of B"=5/4-4/5#
#=9/20#

#:."total shaded area"=3+9/20#
#=69/20#

Q13

I've rotated the original image to make this a bit easier to see.

enter image source here

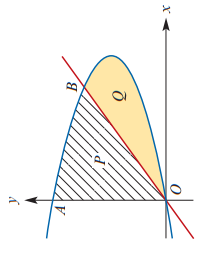If we were given this, we'd integrate with respect to the horizontal (x) axis, then take away some things and get our area.

We can do exactly the same thing here. This time, instead of integrating with respect to x, we integrate with respect to y. This willl give us the area between the curve and the y axis.

a)

to find A, we need the y-intercepts of the curve.

#x=6y-y^2#
Let #x=0#

#6y-y^2=0#
#y(6-y)=0#
#y=0# or #y=6#
We can reject #y=0#, so #A=(0,6)#

B is the interception between #x=6y-y^2# and #x=y#

Solve simultaneously:

#y=6y-y^2#
#5y-y^2=0#
#y(5-y)=0#
#y=5#

Since #y=x, x=5# as well.
#:. B=(5,5)#

b)

The area of P is the area under the curve between A and B, plus the area under the line between B and the origin.

#"area under curve"=int_5^6(6y-y^2)dy#
#=[(6y^2)/2-1/3y^3]_5^6#
#=[3y^2-1/3y^3]_5^6#
#=(3(6)^2-1/3(6)^3)-(3(5)^2-1/3(5)^3)#
#=36-100/3#
#=8/3#

For the area under the line, its easier to treat it like a triangle.

#"area under line"=1/2xx5xx5#
#=25/2#

#:."area of P"=25/2+8/3#
#=91/6#

c)

#"total area under curve"=int_0^6(6y-y^2)dy#
#=[3y^2-1/3y^3]_0^6#
#=(3(6)^2-1/3(6)^3)-0#
#=36#

#:."area of Q"=36-91/6#
#=125/6#

Related questions
Impact of this question
1630 views around the world
You can reuse this answer
Creative Commons License