Prove that Cot 4x (sin 5 x + sin 3 x) = Cot x (sin 5 x - sin 3 x) ?
2 Answers
Right side:
Left side:
They're equal
Factor formula (Sum-to-Product and Product-to-Sum identities)
Explanation:
For this question, we can use the Sum-to-Product and Product-to-Sum identities.
I'm lazy, so here's a picture of the identities.
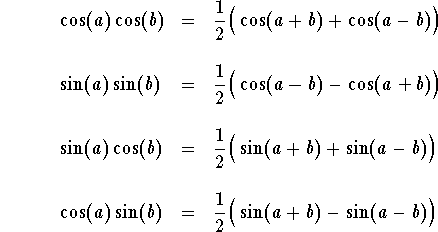
The product-to-sum formula above can be derived via compound angle identities.
Using the substitution
 )
)
So, now that we've got that sorted out, let's apply our formulas.
Alternatively, you could also apply the sum-to-product formula on the right-hand side:


