Calculate the relative permittivity of a KCl crystal at optical frequencies?
KCl has the NaCl crystal structure with a lattice parameter of 0.629 nm. Calculate the relative permittivity of a KCl crystal at optical frequencies given that the electronic polarizability of #"K"^+# is #1.264 xx 10^-40 "F m"^2# and that of #"Cl"^-# is #3.408 xx 10^-40" F m"^2# .
I found a solved example here (not 100% identical): (see example 7.8)
https://ece.uwaterloo.ca/~anis/ece209/tutorial/tutorial_09_ans
thank you all
KCl has the NaCl crystal structure with a lattice parameter of 0.629 nm. Calculate the relative permittivity of a KCl crystal at optical frequencies given that the electronic polarizability of
I found a solved example here (not 100% identical): (see example 7.8)
https://ece.uwaterloo.ca/~anis/ece209/tutorial/tutorial_09_ans
thank you all
1 Answer
It is given that KCl has crystal structure of NaCl. KCl has 4 ion pairs per unit cell. The number of ion pairs per unit volume
#N= 4/a^3#
where#a# is lattice parameter.
Inserting given value we get
#N=4/(0.629xx10^-9)^3 = 1.607 xx10^28\ m^3#
Using Clausius-Mossotti equation which relates the relative permittivity
#(epsilon_r-1)/(epsilon_r+2)=1/(3epsilon_0)(Nalpha_i+N_(Cl)alpha_(eCl)+N_K alpha_(eK))#
where#alpha_i# is the mean ionic polarizability per ion pair, and#epsilon_0# is permittivity of free space.
We see that there is one-to-one ratio between the number of molecules and ions in KCl, we can take all the N’s to be the same. Moreover, at optical frequencies contribution from ionic polarization is not there. Therefore, We consider electronic
polarization of individual ions only. The equation for relative permittivity at optical frequencies becomes
#epsilon_(r(op))=1/(3epsilon_0)(Nalpha_(eCl)+N alpha_(eK))xx(epsilon_(r(op))+2)+1#
#=>epsilon_(r(op))=N/(3epsilon_0)(alpha_(eCl)+alpha_(eK))xxepsilon_(r(op))+(N/(3epsilon_0)(alpha_(eCl)+ alpha_(eK))xx2)+1#
#=>ε_(r(op))=((2N)/(3epsilon_0)(alpha_(eCl)+ alpha_(eK))+1)/(1-N/(3epsilon_0)(alpha_(eCl)+ alpha_(eK)))#
#=>epsilon_(r(op))=(2N(alpha_(eCl)+ alpha_(eK))+3epsilon_0)/(3epsilon_0-N(alpha_(eCl)+ alpha_(eK))#
While taking
Post your work.
.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.
We know that NaCl has a cubic unit cell as shown in the figure below.
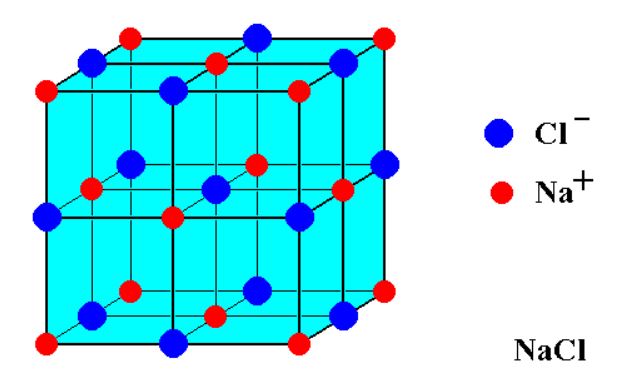
It can be visualized as a face-centered cubic array of anions with an interpenetrating lattice of fcc cation or vice versa. As the size of sodium ions is much smaller than the size of chloride ions, the chloride ions occupy the lattice point.
When counting the number of ions, a corner site is shared by
#"Cl"^(-) =1_"center"+12_"edge"xx1/4=4_"total"#
#"Na"^+=6_"face"xx1/2+8_"corner"xx1/8=4_"total"#
