We wish to expand
#(1+x)(1+x)(1+x)(1+x)=(1+x)^4#
Now, the Binomial Theorem states that it is possible to expand the sum of two numbers #x# and #y# raised to the power #n# into the form:
#(x+y)^n = sum_(k=0)^n ((n),(k))x^ky^(n-k)#
Where #((n),(k))# denotes the binomial coefficient, and is calculated by:
#((n),(k))=(n!)/(k!(n-k)!)#
If we substitute #y=1# into the formula, we have:
#(1+x)^n = sum_(k=0)^n ((n),(k)) x^k#
In our particular case, #n = 4#, hence:
#(1+x)^4 = sum_(k=0)^4 ((4),(k)) x^k=((4),(0))+((4),(1))x+...+((4),(4))x^4#
All that is left to do is calculate #((4),(k))# for #k=1,2,3# and #4#.
#{(((4),(0))=(4!)/(0!*4!)=24/(1*24)=1),(((4),(1))=(4!)/(1!*3!)=24/(1*6)=4),(((4),(2))=(4!)/(2!*2!)=24/(2*2)=6),(((4),(3))=(4!)/(3!*1!)=24/(6*1)=4),(((4),(4))=(4!)/(4!*0!) = 24/(24*1)=1) :}#
Finally,
#(1+x)^4 = 1+4x+6x^2+4x^3+x^4#
For small #n#, calculating every #((n),(k))# explicitly is ok, but for larger values, it's tedious, because the factorial function rapidly increases.
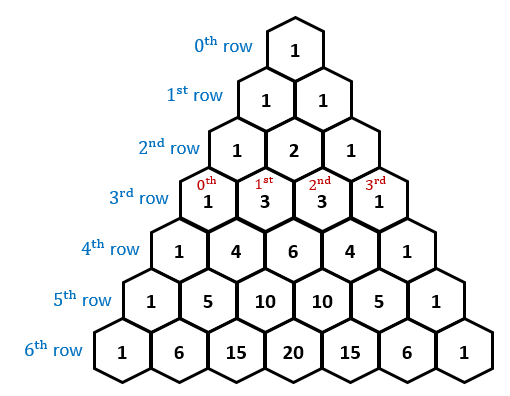
Instead, we might use Pascal's triangle to makes things simpler. Here it is:
 )
)
This triangle is build up by adding; if we imagine near every #1# to be a #0# and if the element at the very top is #1#, then the next row will have elements #0+1=1# and #1+0=1#, because our top #1# has zeros to its right and left. Similarly, the second row values will be #0+1=1#, #1+1=2#, and #1+0=1#.
To see more on Pascal's triangle, check this link.
Another property of this triangle is that the #k#-th element on the #n#-th row is equal to #((n),(k))#. By this knowledge, we can easily judge that
#(1+x)^4 = 1+4x+6x^2+4x^3+x^4#
Here's a visual representation.
![enter image source here]()
 )
)

