How would you solve to find the equation of the tangent line to the curve #for y = (1+x) cos x# at the given point (0,1)?
1 Answer
Jun 30, 2018
Explanation:
First let's verify that
Apply the product rule
Call this slope
Now, the tangent to
Since,
Hence, our tangent has the equation:
We can see the graph of
![enter image source here]
(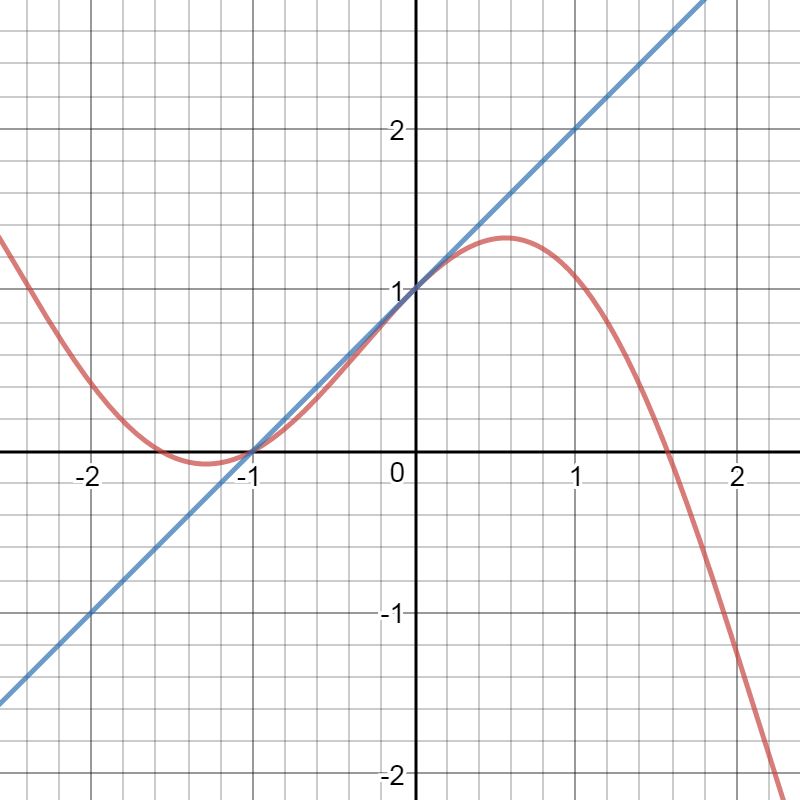 )
)
