Find the length of the median of one of the legs of an isosceles triangle with sides the lengths 18,18,and 6?

1 Answer
sankarankalyanam
Aug 11, 2018

color(maroon)("Length of the median " bar(CD) ~~ 17.75 " units"

Explanation:

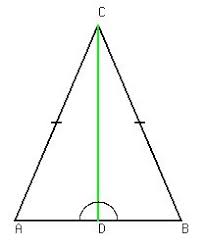
![https://www.algebra.com/algebra/homework/Triangles/Anhttp://-altitude-a-median-and-an-angle-bisector-in-the-isosceles-triangle.lesson](https://useruploads.socratic.org/5yZt5fyJTCaKtATjyjIS_isosceles%20triangle.png)

"Given : " bar(AC) = bar (BC) = 18, AB = 6, " To find median " bar(CD)

Delta ABC " is an isosceles triangle with " bar(CD) " perpendicular bisector of " bar(AB)

Applying Pythagoras theorem,

bar(CD) = sqrt ((AC)^2 - (AD)^2)

bar(AD) = bar(AB) / 2 = 6 / 2 = 3

bar(CD) = sqrt(18^2 - 3^2) ~~ 17.75

Related questions
Impact of this question
4900 views around the world
You can reuse this answer
Creative Commons License