Question #269be
1 Answer
The dilution factor for the fourth tube will be
You know that the dilution factor is defined as the final volume of the sample divided by the initial volume of the sample. So, if you add
and your final volume will be
This means that the dilution factor will be
When you're doing a serial dilution, each tube will dilute the sample by the same calculated dilution factor.
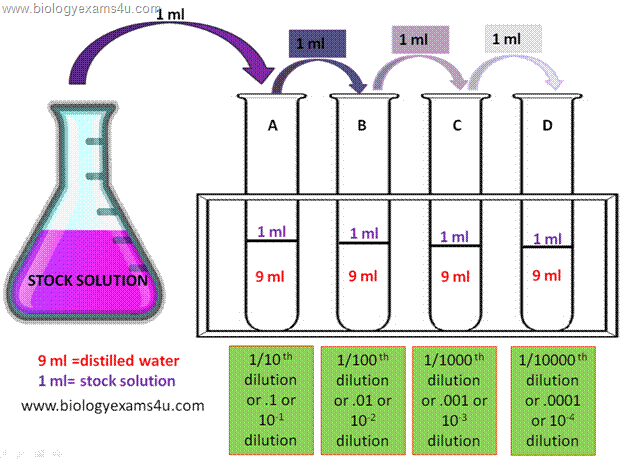
Notice how in the above example each solution will be diluted by a factor of 10. If you apply this method to your dilution, you'll get a dilution factor for tube 4 equal to
The first tube will have a
Now you repeat the process for tubes 3 and 4 to get the final dilution factor of
You can read more on dilution factors and serial dilutions here:
http://socratic.org/questions/how-do-you-calculate-dilution-factor?source=search
http://socratic.org/questions/how-do-you-do-serial-dilution-calculations?source=search

