 )
)
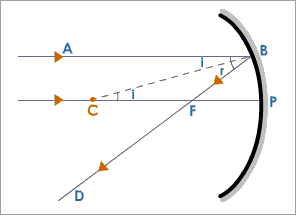
Consider a Concave mirror as shown in the figure above.
A ray of light #AB# traveling parallel to the principal axis #PC# is incident on a convex mirror at #B#. After reflection, it goes through the focus #F#. #P# is the pole of the mirror. #C# is the center of curvature.
The distance #PF=# focal length #f#.
The distance #PC=# radius of curvature #R# of the mirror.
#BC# is the normal to the mirror at the point of incidence #B#.
#∠ABC = ∠CBF# (Law of reflection, #∠i=∠r#)
#∠ABC = ∠BCF# (alternate angles)
#=> ∠BCF = ∠CBF#
#∴ Delta FBC# is an isosceles triangle.
Hence, sides #BF = FC#
For a small aperture of the mirror, the point #B# is very close to the point #P#,
#=> BF = PF#
#∴ PF = FC= 1/2 PC#
#=> f = 1/2 R#
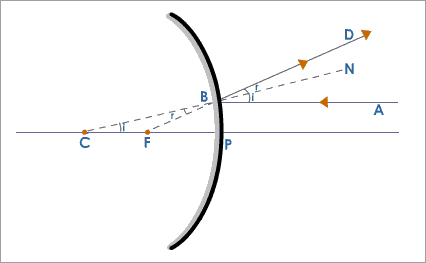
Now consider a Convex mirror as shown in the figure below.
 )
)
A ray of light #AB# traveling parallel to the principal axis #PC# is incident on a convex mirror at #B#. After reflection, it goes to #D# and appear to be coming from the focus #F#.
The distance #PF=# focal length #f#.
The distance #PC=# radius of curvature #R# of the mirror.
Straight line #NBC# is the normal to the mirror at the point of incidence #B#.
#∠ABN = ∠NBD# (Law of reflection, #∠i=∠r#)
#∠CBF = ∠DBN# (vertically opposite angles)
#angleNBA=angleBCF# (corresponding angles)
#=> ∠BCF = ∠CBF#
#∴ Delta FBC# is an isosceles triangle.
Hence, sides #BF = FC#
For a small aperture of the mirror, the point #B# is very close to the point #P#,
#=> BF = PF#
#∴ PF = FC= 1/2 PC#
#=> f = 1/2 R#
Thus, for a spherical mirror (both for a concave and for convex), the focal length is half of radius of curvature.
 )
)  )
) 