We live in three dimensional space. In a Cartesian coordinate system we need three coordinates to uniquely define a point in space, its #(x,y,z).#
Vector is defined as a quantity which has both magnitude and direction.
 )
)
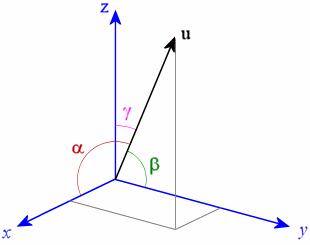
If #vecu# is a vector quantity, we need three angles which it makes with the three axes, as shown in the picture above, to uniquely define it.
If #alpha# is the angle between #vecu# and the #x#-axis,
#beta# is the angle between #vecu# and the #y#-axis and
#gamma# is the angle between #vecu# and the #z#-axis
Then unit vector #hatu# can be written as
#hatu = cos alpha hati + cos beta hatj + cosgamma hatk#
Where #hati, hatj and hatk# are unit vectors in #x,y,z# directions respectively.
And these three cosines are called the direction cosines.
 )
) 