Question

Question #27796

Answer 1

Pascal's law states that pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions throughout the fluid.

Explanation:

Proof
Consider an infinitesimal element of fluid in the form of a triangular prism containing a point `P` of interest as shown in the figure below.

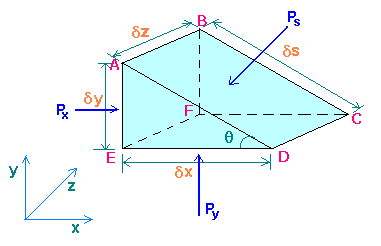
Let the pressures `P_x` along `x` axis, `P_y` along `y` axis, and `P_s` normal to any plane inclined at any angle `theta` to the horizontal at this point be acting as shown.

There can be no shearing forces for a fluid in equilibrium. As such the sum of the forces in any direction must be zero. The forces acting are due to the pressures on the surrounding and the gravity.

Knowing the definition of pressure and that `x and y` axes are orthogonal to each other, sum of forces in the `x`-direction is

`P_x xxdeltayxxdeltaz +( - P_sxxdeltazxxdeltas sin theta) = 0`
`=>P_x xxdeltayxxdeltaz-Psxxdeltasxxdeltazxx(deltay)/(deltas)=0`
`=>P_x xxdeltayxxdeltaz-Psxxdeltazxxdeltay=0`
`=>P_x = P_s` .....(1)

Sum of forces in the `y`-direction including weight of the fluid element is
`P_y xxdeltax xxdeltaz +( - P_sxxdeltazxxdeltas cos theta) +(-"specific gravity"xx "Volume"xxg)= 0`
`=>P_y xxdeltax xxdeltaz - P_sxxdeltazxxdeltas (deltax)/(deltas)`
`-rhoxx 1/2deltax xxdeltayxxdeltazxxg= 0`

Since `deltax, deltay and deltaz` are infinitesimal; therefore, the last term which is product of three infinitesimals can be ignored in comparison to first two terms which is product of two infinitesimals. We have
`P_y xxdeltax xxdeltaz - P_sxxdeltazxxdeltax = 0`
`=>P_y = P_s` .....(2)

From (1) and (2) we get
`P_x = P_y=P_s` .....(3)
By selecting orientation of coordinate system appropriately the above expression could be extended to include the `z`-axis.
`:.P_x = P_y=P_z`

In the limiting case the element can be considered a point so the derived expression indicates that pressure at any point is the same in all directions.