Question #74b2b

Question

Question #74b2b

1 Answer

Impact of this question

6194 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-01T07:54:53

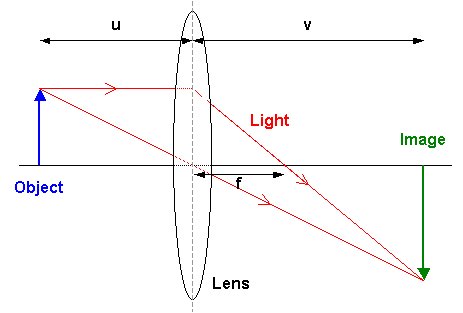
www.doitpoms.ac.uk

We know the conjugate foci relation of lens as follows

$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$ $color(blue)(1/v-1/u=1/f)$

Where

$u \to object distance$ $u->"object distance"$

$v \to image distance$ $v->"image distance"$

$f \to focal length$ $f->"focal length"$

Imposing sign convention

$u = - u for real object$ $u=-u" for real object"$

$v = + v for real image$ $v=+v" for real image"$

$f = + f for converging lens$ $f=+f" for converging lens"$

So the lens formula becomes

$\frac{1}{v} - \frac{1}{- u} = \frac{1}{f}$ $color(green)(1/v-1/(-u)=1/f)$

$\Rightarrow \frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ $=>color(green)(1/v+1/u=1/f)$

Now let us consider that the distance between real object and real image be $D$ $D$ . This means $u + v = D$ $u+v=D$ . So putting $v = D - u$ $v=D-u$ in the lens equation we get

$\frac{1}{D - u} + \frac{1}{u} = \frac{1}{f}$ $color(red)(1/(D-u)+1/u=1/f)$

$\Rightarrow \frac{u + D - u}{u (D - u)} = \frac{1}{f}$ $color(red)(=>(u+D-u)/(u(D-u))=1/f)$

$\Rightarrow D f = (u (D - u))$ $color(red)(=>Df=(u(D-u)))$

$\Rightarrow u^{2} - D u + D f = 0$ $color(red)(=>u^2-Du+Df=0)$

This is a quadratic equation of $u$ $u$ . For the formation of real images for real object the roots of this equation should be real.To satisfy this condition the discriminant of this equation must be $\geq 0$ $>=0$

So $D^{2} - 4 D f \geq 0$ $color(violet)(D^2-4Df>=0)$

$\Rightarrow D^{2} \geq 4 D f$ $color(violet)(=>D^2>=4Df)$

$\Rightarrow D \geq 4 f$ $color(violet)(=>D>=4f)$

From this relation we can conclude that the minimum distance between real obejct and its real image formed by a converging lens is $4 f$ $4f$

The following graph supports the phenomenon discussed above.

google

Science

Math

Humanities

... and beyond

Question #74b2b

1 Answer

Related questions

Impact of this question