Question

A force field is described by `<F_x,F_y,F_z> = < xy , xy-x, 2y -zx >`. Is this force field conservative?

Answer 1

The force field is not conservative, `curl(vecF)!=vec0`.

Explanation:

If `vecF` is a vector (force) field in `RR^3`, then the curl of `vecF` is the vector `curl(vecF)` and is written as `gradxxvecF`. The vector field `vecF` is conservative iff `vecF=gradf` for some potential function. If `vecF` is conservative, `curl(vecF)=vec0`. However, this does not mean that a vector field with `curl=vec0` is absolutely conservative; the vector field must also have a potential function to be conservative, but the first prerequisite is that `curl(vecF)=vec0`.

As stated above, the curl is given by the cross product of the gradient of `vecF` (in the form `< P, Q, R >`) and itself.


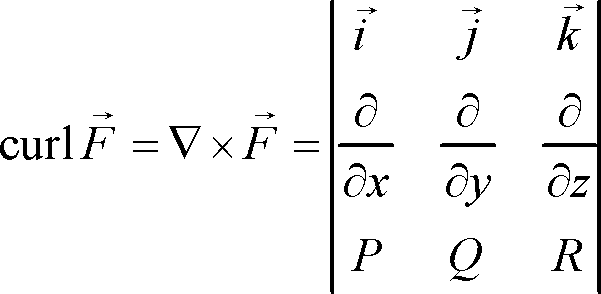
We have `vecF=< xy, xy-x, 2y-zx >` where

`P=xy`

`Q=xy-x`

`R=2y-zx`

The curl of the vector field is then given as:

We take the cross product as we usually would, except we'll be taking partial derivatives each time we multiply by a partial differential.

For the `veci` component, we have `del/(dely)(2y-zx)-del/(delz)(xy-x)`

`=>(2-0)=2`

We can tell immediately that the product will not be `vec0`, but we can finish the process.

For the `vecj` component, we have `del/(delx)(2y-zx)-del/(delz)(xy)`

`=>-(-z-0)=z`

(Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is `0` as we treat all other variables as constants)

For the `veck`component, we have `del/(delx)(xy-x)-del/(dely)(xy)`

`=>(y-1-x)=y-1-x`

This gives a final answer of `curl(vecF)=<2,z,y-x-1> !=vec0`

`:.` Force field is not conservative