Question

A projectile is shot from the ground at an angle of `pi/4` and a speed of `3 /5 m/s`. Factoring in both horizontal and vertical movement, what will the projectile's distance from the starting point be when it reaches its maximum height?

Answer 1

Consider,

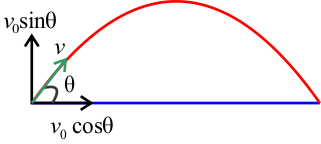
where `theta = pi/4 = 45°` in this case.

Moreover, recall that `nu = 0` at the maximum of the parabolic movement.

`nu = nu_0 + at`
`=> t = (nu - nu_0)/g`

`therefore t = (0 - (0.6m)/ssin(45°))/((-9.8m)/s^2) approx 4.32*10^-2s`

Now: let's understand the horizontal displacement of the projectile. Recall,

`Deltax = nu_0costheta * t`

Hence,

`Deltax = (0.6m)/scos(45°) * 4.32*10^-2s approx 2.60*10^-2m`

This is fairly reasonable, `(0.6m)/s` is very slow.