A tank of gas has partial pressures of nitrogen and oxygen equal to 1.61 xx 10^4 "kPa" and 4.34 xx 10^5 "kPa", respectively. What is the total pressure of the tank?

1 Answer
Stefan V.
Jun 12, 2017

4.50 * 10^5 "kPa"

Explanation:

The idea here is that when the volume and the temperature of a gaseous mixture are kept constant, the total pressure of the mixture is equal to the sum of the partial pressures of its gaseous components -> this is known as Dalton's Law of Partial Pressures.

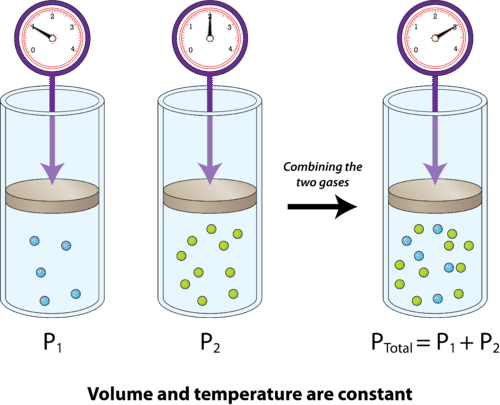
![https://www.ck12.org/book/CK-12-Chemistry-Concepts-Intermediate/section/14.12/](https://useruploads.socratic.org/ANYt1puRl6jzbxWaGHJO_f-d%253Aaa7b820f730dd7f29451dcf420a450b9a418da33562c64772ef80c33%252BIMAGE_THUMB_POSTCARD_TINY%252BIMAGE_THUMB_POSTCARD_TINY.1)

In your case, you know that the mixture contains nitrogen gas, "N"_2, and oxygen gas, "O"_2, which means that the total pressure of the mixture will be

P_"total" = P_ ("N" _ 2) + P_ ("O"_ 2)

Plug in your values to find

P_"total" = 1.61 * 10^4color(white)(.)"kPa" + 4.34 * 10^5color(white)(.)"kPa"

P_"total" = color(darkgreen)(ul(color(black)(4.50 * 10^5color(white)(.)"kPa")))

The answer is rounded to two decimal places, the number of decimal places you have for your values.

Related questions
See all questions in Partial Pressure
Impact of this question
5725 views around the world
You can reuse this answer
Creative Commons License