Question

A truck pulls boxes up an incline plane. The truck can exert a maximum force of `2,800 N`. If the plane's incline is `(3 pi )/8` and the coefficient of friction is `1/7`, what is the maximum mass that can be pulled up at one time?

Answer 1

The mass is `=292.0 kg`

Explanation:


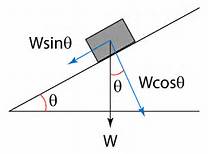
Resolving in the direction parallel to the plane `↗^+`

Let the force exerted by the truck be `F=2800N`

Let the frictional force be `=F_rN`

The coefficient of friction `mu=F_r/N=1/7`

The normal force is `N=mgcostheta`

The angle of the plane is `theta=3/8pi`

The acceleration due to gravity is `g=9.8ms^-2`

Therefore,

`F=F_r+mgsintheta`

`=muN+mgsintheta`

`=mumgcostheta+mgsintheta`

`m=F/(g(mucostheta+sintheta))`

`=2800/(9.8(1/7*cos(3/8pi)+sin(3/8pi))`

`=292.0kg`