According to Kinetic Molecular Theory, the collision frequency is equal to the root-mean-square velocity of the molecules divided by their mean free path.
#color(blue)(bar(ul(|color(white)(a/a)ν = v_"rms"/λcolor(white)(a/a)|)))" "#
Root-mean-square velocity
The formula relating the rms velocity to the temperature and molar mass is:
#color(blue)(bar(ul(|color(white)(a/a) v_"rms" = sqrt((3RT)/M)color(white)(a/a)|)))" "#
where
# R# = the Universal Gas Constant
#T# = the temperature
#M# = the molar mass
For #"H"_2# at 24 °C,
#T = "(24 + 273.15) K" = "297.15 K"#
#M = "2.016 g·mol"^"-1" = 2.016 × 10^"-3"color(white)(l) "kg·mol"^"-1"#
#v_"rms" = sqrt((3RT)/M) = sqrt((3 × 8.314 color(red)(cancel(color(black)("J·K"^"-1""mol"^"-1"))) × 297.15 color(red)(cancel(color(black)("K"))))/( 2.016 × 10^"-3" color(red)(cancel(color(black)("kg·mol"^"-1")))) × ( 1 color(red)(cancel(color(black)("kg")))·"m"^2"s"^"-2")/(1 color(red)(cancel(color(black)("J"))))) = = "1917 m·s"^"-1"#
The mean free path
If the molecules have diameter d, then we can use a circle of diameter #σ = 2d# to represent a molecule's effective collision area.
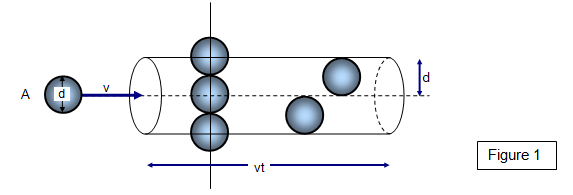
For a hydrogen molecule, #σ = "289 pm"#.
The formula for the mean free path is
#color(blue)(bar(ul(|color(white)(a/a) λ = (RT)/(sqrt2πσ^2N_"A"P)color(white)(a/a)|)))" "#
#R = 0".083 14 bar·L·K"^"-1""mol"^"-1" = 8.314 × 10^"-5"color(white)(l)"bar·m"^3·"K"^"-1""mol"^"-1"#
#T = "297.15 K"#
#σ = "289 pm" = 289 × 10^"-12"color(white)(l) "m"#
#N_"A" = 6.022 × 10^23color(white)(l) "mol"^"-1"#
#P = "2.00 bar"#
#λ = (RT)/(sqrt2πσ^2N_"A"P) = (8.314 × 10^"-5"color(red)(cancel(color(black)("bar")))·stackrelcolor(blue)("m")(color(red)(cancel(color(black)("m"^3))))·color(red)(cancel(color(black)("K"^"-1""mol"^"-1"))) × 297.15 color(red)(cancel(color(black)("K"))))/(sqrt2π × (289 × 10^"-12" color(red)(cancel(color(black)("m"))))^2 × 6.022 × 10^23 color(red)(cancel(color(black)("mol"^"-1"))) × 2.00 color(red)(cancel(color(black)("bar"))))#
#= 5.52 × 10^"-8"color(white)(l) "m" = "55.2 nm"#
Collision frequency
#ν = v_"rms"/λ = (1917 color(red)(cancel(color(black)("m")))·"s"^"-1")/(5.52 × 10^"-8" color(red)(cancel(color(black)("m")))) = 3.46 × 10^10color(white)(l) "s"^"-1"#


