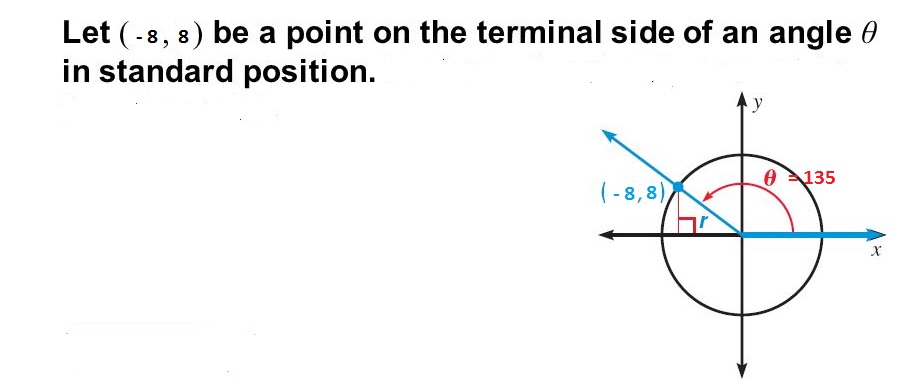
Given point (-8,8) how do you find the distance of the point from the origin, then find the measure of the angle in standard position whose terminal side contains the point?

Question

3470 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-19T08:19:56

Measure of the angle $theta = 135^@$ or $((3pi)/4)^c$

Distance formula : $d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)$

Given point $A (-8, 8)$ and Origin $O (0,0)$

$vec(OA) = r = sqrt ((-8)^2 + 8^2) = sqrt 128 = 8sqrt2$

$x = r cos theta$ , $y = r sin theta$

$- 8 = 8 sqrt2 cos theta$

$cos theta = -cancel8 / (cancel8 sqrt2) = -1/sqrt2$ or $theta =color(purple)( - pi/4 = (pi - pi/4) = (3pi)/4$

Similarly, $8 sqrt2 sin theta = 8$

$sin theta = 8 / (8 sqrt2) = 1/sqrt2$ or $theta = pi/4$ or = $pi - pi/4) = (3pi)/4$

Slope of the line $m = tan theta = -8 / 8 = -1$

$x$ $(-)$ and $y$ $(+)$ in II quadrant.

Hence $theta = tan ^-1 (-8/8) = tan^-1 -1 = -1 = (3pi)/4$

enter image source here
( useruploads.socratic.org )