How do you find the slope and intercept of $y=-x-7$ ?

Question

19930 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-03T06:38:38

Slope: -1

x-intercept: (-7, 0)

y-intercept: (0, -7)

$y = -x - 7$

This equation is in slope-intercept form:
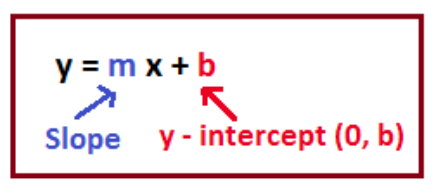
www.geogebra.org

Based on the image, we know that the slope is the value multiplied by $x$ , so the slope is $-1$ .

We know the $y$ -intercept is $b$ , or $-7$ , so it is at $(0, -7)$ .

To find the $x$ -intercept, plug in $0$ for $y$ and solve for $x$ :
$0 = -x - 7$

$7 = -x$

$x = -7$

The $x$ -intercept is at $(-7, 0)$ .'

Hope this helps!

Answer 2 · 2018-08-04T00:08:41

Slope $-1$ , $y$ -int $-7$ , $x$ -int $-7$

The good thing is that this equation is in slope-intercept form

$y=mx+b$ , with slope $m$ and a $y$ -intercept of $b$ .

By pattern matching, we see that our slope is $-1$ , and our $y$ -intercept is $-7$ .

We can find our $x$ -intercept by setting $y$ equal to zero. We get

$-x-7=0=>-x=7=>x=-7$

Therefore, our slope is $-1$ , our $y$ -intercept is $-7$ , and our $x$ -intercept is $-7$ .

Hope this helps!

How do you find the slope and intercept of y=-x-7y=-x-7?