Multiply both side by #3 + 4cos(theta)#:
#3r + 4rcos(theta) = 12#
Substitute x for #rcos(theta)#:
#3r + 4x = 12#
Subtract 4x from both sides:
#3r = 12 - 4x#
Square both sides:
#9r^2 = 144 - 96x + 16x^2#
Substitute #9x^2 + 9y^2# for #9r^2#:
#9x^2 + 9y^2 = 144 - 96x + 16x^2#
Move everything but the constant to the left and subtract #7h^2# from both sides:
#-7x^2 + 96x - 7h^2 + 9(y - 0)^2 = 144 - 7h^2#
Complete the square for the x term:
#-7(x^2 - 96/7x + h^2) + 9(y - 0)^2 = 144 - 7h^2#
#-2hx = -96/7x#
#h = 48/7#
#-7(x - 48/7)^2 + 9(y - 0)^2 = -1296/7#
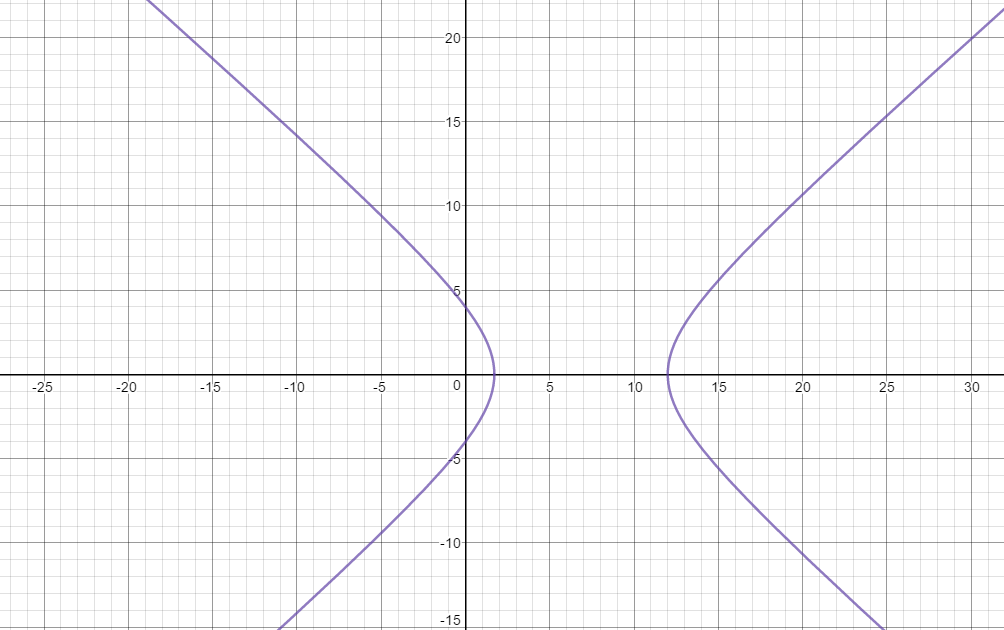
#(x - 48/7)^2/(36/7)^2 - (y - 0)^2/(12sqrt(7)/7)^2 = 1#
Center#(48/7, 0)#
#x_1 = 48/7 - 36/7 = 12/7#
#x_2 = 48/7 + 36/7 = 12#
Vertices: #(12/7, 0) and (12,0)#
#b/a = (12sqrt(7)/7)/(36/7) = sqrt(7)/3#
asymptotes:
#y = -(sqrt(7)/3)(x - 48/7)#
#y = (sqrt(7)/3)(x - 48/7)#
Here is the graph:
 )
)
 )
) 