Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region `x=y^2`, `y=0`, and `y=sqr2` rotated about the x axis?

Answer 1

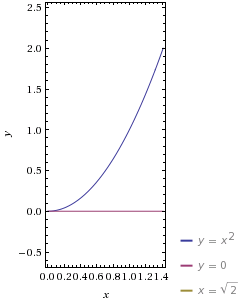
It's unclear what your solid is, but the only one that makes sense is `y = sqrt2` and not `y = 0` because `y = 0` is redundant when you are rotating about the x-axis. Maybe you meant to emphasize that it is `y = sqrtx` and not `y = -sqrtx`. Assuming that:

`x = y^2 -> y = sqrtx`
You only need the positive one since `y = 0` is a boundary, and is also your axis of rotation. Thus, you are looking at this:


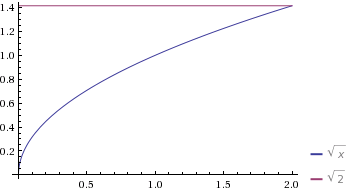
Since the shell method implies you are rotating about the y-axis (which is inconvenient for the regular revolution method), we can rewrite this for that.

`x = y^2 -> y = x^2 in [0, oo)` (only positive `x`)
`y = 0 -> x = 0`
`y = sqrt2 -> x = sqrt2`

Now we really just have `y = x^2` in the first quadrant rotated around the y-axis, stopped at `x = sqrt2`, intersecting at `(sqrt2, 2)`. Which is:


The shell method is:

`int_a^b 2pixf(x)dx`

where:
`2pi` is the radian measure for the "circumference" of the shape
`x` is the radius of the shell
`f(x)` is the height of the shell

`V = 2piint_0^sqrt2 x(x^2)dx`

`= 2pi (x^4/4)|_(0)^sqrt2`

`= 2pi ((sqrt2)^4/4 - 0^4/4)`

`= 2pi (1)`

`= color(blue)(2pi "rad")`