How many milliliters of 12.0 M #HCl(aq)# must be diluted with water to make exactly 500. mL of 3.00 M hydrochloric acid?
1 Answer
Explanation:
Your strategy here will be to use the molarity and volume of the diluted solution to determine how many moles of solute, which in your case is hydrochloric acid,
Once you know this value, you an sue the molarity of the stock solution as a conversion factor to see how many milliliters would contain this many moles.
The underlying principle of a dilution is the fact that the number of moles of solute must remain constant. Basically, a dilution decreases the concentration of a solution by increasing its volume.
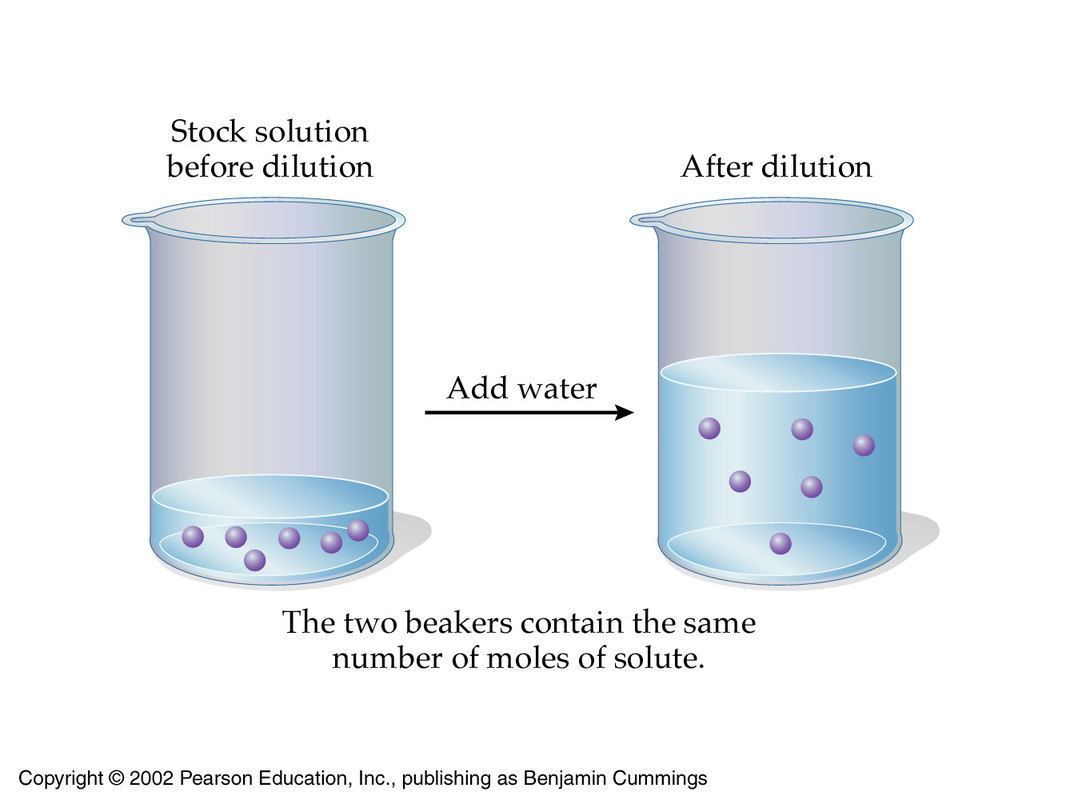
As you know, a solution's molarity tells you how many moles of solute you get per liter of solution. The diluted solution has a molarity of
In your case, the
#500. color(red)(cancel(color(black)("mL"))) * (1color(red)(cancel(color(black)("L"))))/(10^3color(red)(cancel(color(black)("mL")))) * "3.00 moles HCl"/(1color(red)(cancel(color(black)("L")))) = "1.5 moles HCl"#
Now use the molarity of the stock solution to determine how many milliliters would contain
#1.5 color(red)(cancel(color(black)("moles"))) * "1 L"/(12.0color(red)(cancel(color(black)("moles")))) * (10^3color(white)(a)"mL")/(1color(red)(cancel(color(black)("L")))) = color(green)(|bar(ul(color(white)(a/a)"125 mL"color(white)(a/a)|)))#
The answer is rounded to three sig figs.
ALTERNATIVE APPROACH
You can get the same result by using the equation for dilution calculations, which looks like this
#color(blue)(overbrace(c_1 xx V_1)^(color(red)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(red)("moles of solute in diluted solution"))#
Here you have
Rearrange to solve for
#c_1V_1 = c_2V_2 implies V_1 = c_2/c_1 * V_2#
#V_1 = (3.00 color(red)(cancel(color(black)("M"))))/(12.0color(red)(cancel(color(black)("M")))) * "500. mL" = color(green)(|bar(ul(color(white)(a/a)"125 mL"color(white)(a/a)|)))#

