Question

How would you prove that the area of an equilateral triangle constructed on the hypotenuse of a right triangle is equal to the sum of the areas of the equilateral triangles constructed on the legs?

Answer 1

As proved.

Explanation:

Statement of 'Pythagoras theorem': In a right triangle the area of the square on the hypotenuse is equal to the sum of the areas of the squares of its remaining two sides.

`:. a^2 + b^2 = c^2`


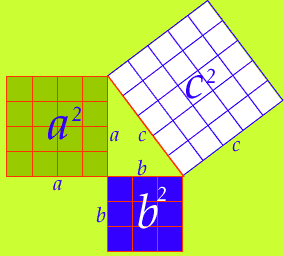
Now let's replace the a, b, c squares by equilateral triangles of sides a, b, c.

`"Given ; "a^2 + b^2 = c^2, " from the right triangle"`

Area of equilateral triangle on hypotenuse c `A_c = (sqrt3/4) c^2`

Similarly, `area of equilateral triangle on side a`A_a = (sqrt3/4) a^2

Likewise, `area of equilateral triangle on side a`A_b = (sqrt3/4) b^2

`A_a + A_b = (sqrt3/4)a^2 + (sqrt3/4)b^2`

`=> (sqrt3/4) (a^2 + b^2) = (sqrt3/4) c^2`