Schrodinger equation in 1 dimension Question details in the image?
In this image E = V + KE
KE = #1/2mv^2#
can you prove from this
#DeltaxDeltap >= h/(4pi)#
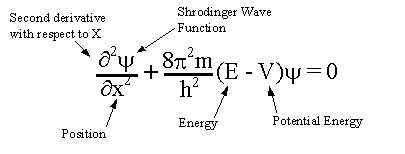
I try to solve this but instead end up proving that probablity of finding electron in all space is 1
#p^2 * ψ^2 = p^2#
This is the Schrodinger equation in 1 dimension
I'm trying to prove this from various forms of the Schrodinger equation
In this image E = V + KE
KE =
can you prove from this

I try to solve this but instead end up proving that probablity of finding electron in all space is 1
This is the Schrodinger equation in 1 dimension
I'm trying to prove this from various forms of the Schrodinger equation
1 Answer
Starting from
#DeltaxDeltap_x >= ℏ"/"2#
isn't actually enlightening. In fact it adds hours of pain and suffering because you have to derive it from scratch to find the form
#DeltaxDeltap_x >= 1/2 |i << psi | [hatx"," hatp_x] | psi >> |# where
#[hatx, hatp_x] = hatxhatp_x - hatp_xhatx = iℏ# .
That would have shown that for normalized wave functions,
#DeltaxDeltap_x >= 1/2 |i cdot i ℏ |#
#>= ℏ/2 sqrt(i^"*"i)#
#>= ℏ/2#
Just know that the operators are:
#hatx = x#
#hatp_x = -iℏd/dx#
which satisfy
This is consistent with any Schrodinger equation in one Cartesian dimension, and is easy to prove. In fact, I have done it several times, and here is one of those times.
Here is an easy proof to go from here...
We know:
#p = mv# #K = 1/2mv^2#
Thus,
#hatK = hatp^2/(2m) = (-iℏ)^2 /(2m) del^2/(delx^2) = -ℏ^2/(2m) (del^2)/(delx^2)#
So for any Schrodinger equation in one Cartesian dimension...
#hatH psi = Epsi#
#= (hatK + hatV)psi#
#= (-ℏ^2/(2m) (del^2)/(delx^2) + hatV)psi#
Thus,
#-ℏ^2/(2m) (del^2psi)/(delx^2) + hatVpsi = Epsi#
#(del^2psi)/(delx^2) - (2m)/(ℏ^2)[hatV-E]psi = 0#
#(del^2psi)/(delx^2) + (2m)/(ℏ^2)[E-hatV]psi = 0#
#color(blue)((del^2psi)/(delx^2) + (8pi^2m)/(h^2)[E-hatV]psi = 0)#
This of course does NOT tell us what the potential is. That's your responsibility to tell us.

