Is #f(x)=-2x^3-2x^2+8x-1# concave or convex at #x=3#?
1 Answer
Feb 8, 2016
Concave (sometimes called "concave down")
Explanation:
Concavity and convexity are determined by the sign of the second derivative of a function:
- If
#f''(3)<0# , then#f(x)# is concave at#x=3# . - If
#f''(3)>0# , then#f(x)# is convex at#x=3# .
To find the function's second derivative, use the power rule repeatedly.
#f(x)=-2x^3-2x^2+8x-1#
#f'(x)=-6x^2-4x+8#
#f''(x)=-12x-4#
The value of the second derivative at
#f''(3)=-12(3)-4=-40#
Since this is
These are the general shapes of concavity (and convexity):
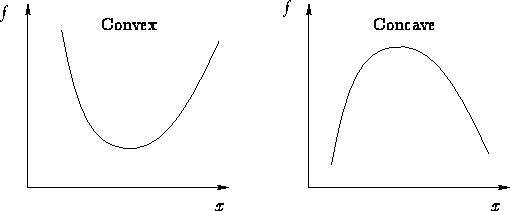
We can check the graph of the original function at
graph{-2x^3-2x^2+8x-1 [-4,4, -150, 40]}

