Question

Please send q 15?

Answer 1

The answer is `=1A`

Explanation:

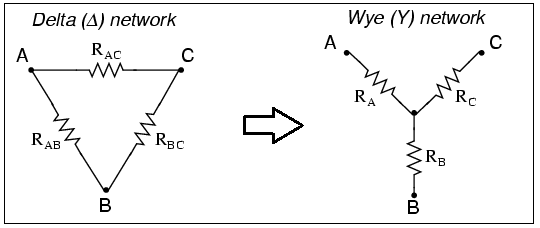
Apply the `Y-Delta` transformation to the `3` resistors on the `RHS`

That is `R_1=50 Omega`, `R_3=15 Omega` and `R_2=20 Omega`

`R_a=(R_1R_2)/(R_1+R_2+R_3)=(50*20)/(50+15+20)=1000/85=11.76 Omega`

`R_b=(R_2R_3)/(R_1+R_2+R_3)=(20*15)/(4+15+10)=300/85=3.53Omega`

`R_c=(R_3R_1)/(R_1+R_2+R_3)=(50*15)/(4+15+10)=750/85=8.82Omega`

`i_1+i_2=1.4A`

and

`U=(R_c+4)i_2=(R_b+10)i_2`

Therefore,

`(8.82+10)(1.4-i_1)=(7.53)*i_2`

Solving for `i_1`

`18.82*1.4-18.82i_2=7.53i_2`

`i_2=26.35/26.35=1.0A`

Answer 2

`"1.0 A"`

Explanation:

Ratio of `"R"_1` and `"R"_2` is

`"R"_1/"R"_2 = "20 Ω"/"50 Ω" = 2/5`

Ratio of `"R"_3` and `"R"_4` is

`"R"_3/"R"_4 = "4 Ω"/"10 Ω" = 2/5`

As the ratio is same in both the cases it’s a balanced Wheatstone bridge. Therefore, `"15 Ω"` resistance can be neglected.

Circuit now:

In series, resistances are added. So the circuit now is

Let `"i"_1` be the current passing through `"24 Ω"` and `"i"_2` be the current passing through `"60 Ω"`. Then,

`"Current" ∝ 1/"Resistance" color(white)(...)[∵ "V = constant"]`

`"i"_1/"i"_2 = "60 Ω"/"24 Ω" = 5/2`

`"i"_1 = 5/(5 + 2) × "1.4 A" = "1.0 A"`

`"i"_2 = 2/(5 + 2) × "1.4 A" = "0.4 A"`

∴ Current passing through `"4 Ω"` and `"20 Ω"` is `"1.0 A"`.