Let #u=x-1#. We can then rewrite the left hand side of the equation as
#sqrt(u+4-4sqrt(u)) + sqrt(u+9-6sqrt(u))#
#=sqrt((sqrt(u)-2)^2) + sqrt((sqrt(u)-3)^2)#
#=|sqrt(u)-2| + |sqrt(u)-3|#
Note the presence of #sqrt(u)# in the equation and that we are only looking for real values, so we have the restriction #u >= 0#. With that, we will now consider all remaining cases:
Case 1: #0 <= u <= 4#
#|sqrt(u)-2| + |sqrt(u)-3| = 1#
#=> 2-sqrt(u) + 3-sqrt(2) = 1#
#=> -2sqrt(u) = -4#
#=> sqrt(u) = 2#
#=> u = 4#
Thus #u=4# is the only solution in the interval #[0, 4]#
Case 2: #4 <= u <= 9#
#|sqrt(u)-2| + |sqrt(u)-3| = 1#
#=> sqrt(u)-2 + 3 - sqrt(u) = 1#
#=> 1=1#
As this is a tautology, every value in #[4, 9]# is a solution.
Case 3: #u >= 9#
#|sqrt(u)-2| + |sqrt(u)-3| = 1#
#=> sqrt(u) - 2 + sqrt(u) - 3 = 1#
#=> 2sqrt(u) = 6#
#=> sqrt(u) = 3#
#=> u = 9#
Thus #u = 9# is the only solution in the interval #[9, oo)#
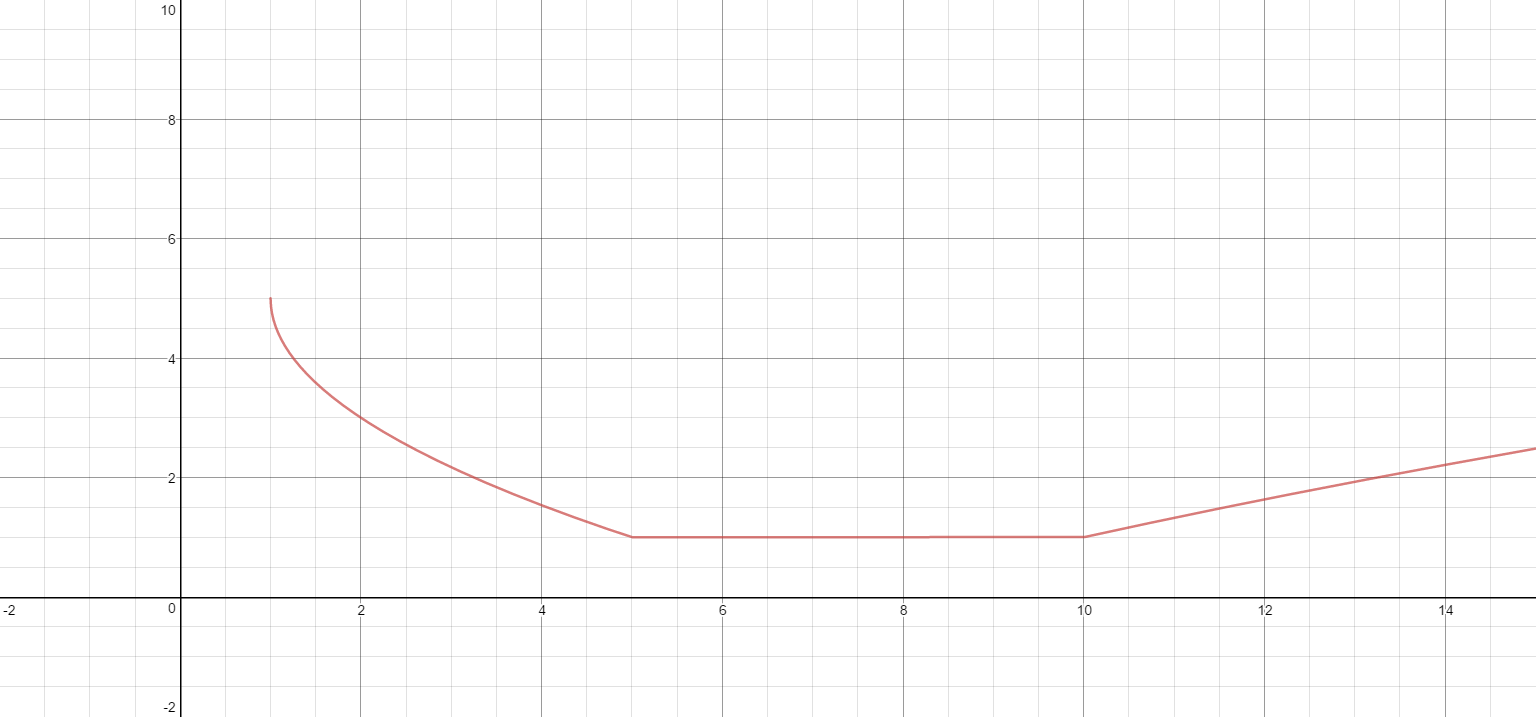
Taken together, we have #[4, 9]# as the solution set for real values of #u#. Substituting in #x = u+1#, we arrive at the final solution set #x in [5, 10]#
Looking at the graph of the left hand side, this matches with what we would expect:
 )
)
 )
) 
