Question

Solve question 80 ?

Answer 1

Answer is "half the". While perimeter of a triangle is greater than sum of its medians, sum of its medians is greater than half the perimeter.

Explanation:

Let us consider `DeltaABC` as shown below, where `AD` is the median which is extended to `P` so that `AD=DP` and `CP` is joined. We also have two other medians `BE` and `CF`.

Now it is easy to prove that `DeltaABD-=DeltaPCD` as `BD=DC`, `AD=DP` and `m/_ADB=m/_CDP` and hence `AB=CP` and `AP=2AD`

Now consider `DeltaACP`. As in a triangle, sum of two sides is always greater than the third, we have `AC+CP>AP`

or `AC+AB>2AD` i.e. some of two sides is greater than twice the median to the third side.

Similarly we have `AB+BC>2BE` and `AC+BC>2CF`.

Adding the three, we get

`2(AB+BC+AC)>2(AD+BE+CF)`

or `AB+BC+AC>AD+BE+CF`

However, also consider `DeltaCFA` and observe that

`AC<AF+CF` or `AC<1/2AB+CF`

Similarly in `DeltaBFC` `BC<BF+CF` or `BC<1/2AB+CF`

adding the two we get `AC+BC<AB+2CF`

or `2CF>AC+BC-AB`

Similarly we can have `2BE>AB+BC-AC`

and `2AD>AB+AC-BC`

adding the three we get

`2(AD+BE+CF)>AB+AC+BC`

or `AD+BE+CF>1/2(AB+AC+BC)`

Hence, while perimeter of a triangle is greater than sum of its medians, sum of its medians is greater than half the perimeter.

Answer 2

jwilson.coe.uga.edu

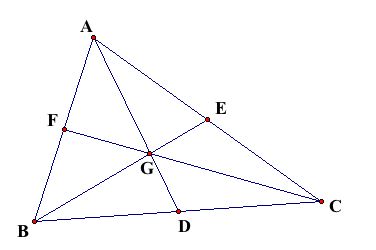
In `DeltaABC,F,DandE` are mid points of `AB,BCandCA` respectively. So `AD,BEandCF` are three medians.

Now

• for `DeltaABD`
  `AD+BD>AB.....[1]`

• for `DeltaBCE`
  `BE+CE>BC.....[2]`

• for `DeltaACF`
  `CF+AF>CA.....[3]`

Adding [1],[2],[3] we get

`(AD+BE+CF)+(BD+CE+AF)>AB+BC+CA`

`=>(AD+BE+CF)+1/2(BC+CA+AB)>AB+BC+CA`

`=>(AD+BE+CF)>1/2(AB+BC+CA)`

So

`"sum of medians">1/2"perimeter"`