Question

What is the area of an equilateral triangle with a 9-inch perimeter?

Answer 1

`(9sqrt3)/4` `"in"^2`

Explanation:


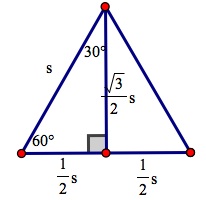
We can see that if we split an equilateral triangle in half, we are left with two congruent equilateral triangles. Thus, one of the legs of the triangle is `1/2s`, and the hypotenuse is `s`. We can use the Pythagorean Theorem or the properties of `30˚-60˚-90˚` triangles to determine that the height of the triangle is `sqrt3/2s`.

If we want to determine the area of the entire triangle, we know that `A=1/2bh`. We also know that the base is `s` and the height is `sqrt3/2s`, so we can plug those in to the area equation to see the following for an equilateral triangle:

`A=1/2bh=>1/2(s)(sqrt3/2s)=(s^2sqrt3)/4`

In your case, the perimeter is `9` inches, so each side of the triangle is `3` inches.

Plug this into the area equation we determined:

`(3^2sqrt3)/4=(9sqrt3)/4` `"in"^2`