What is the final volume when 2.50 mL of a 11.0 M #HCl# solution is diluted to 0.100 M #HCl# solution?
1 Answer
Explanation:
The thing to remember when diluting a solution is that you can determine the dilution factor by using the concentrations or the volumes of the stock and target solutions.
The underlying principle of a dilution is that the concentration of the solution is decreased by increasing its volume while keeping the number of moles of solute constant.
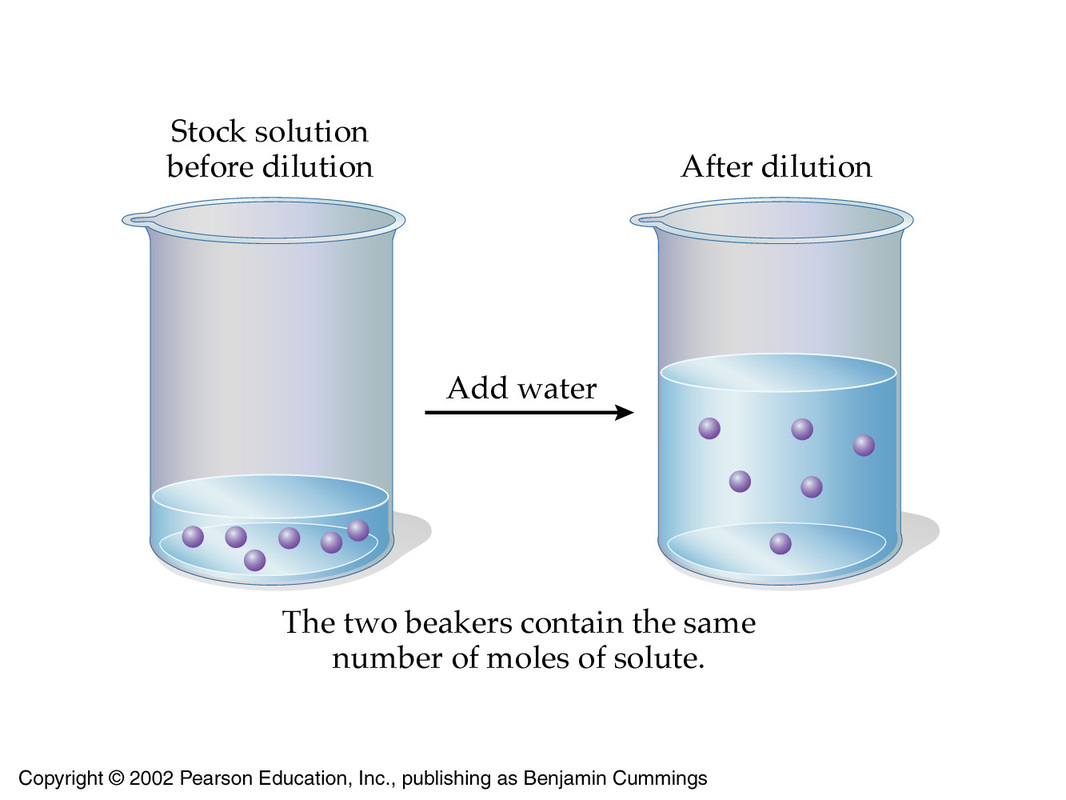
You can express this by using molarities and volumes
#color(blue)(overbrace(c_1 xx V_1)^(color(green)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(green)("moles of solute in diluted solution"))#
Here
Now, you can find a solution's dilution factor be rearranging the above equation to get
#c_1V_1 = c_2V_2 implies c_1/c_2 = V_2/V_1#
This will be the solution's dilution factor
#color(blue)(|bar(ul(color(white)(a/a)"D.F." = c_1/c_2 = V_2/V_1color(white)(a/a)|)))#
In essence, the dilution factor tells you how much higher the concentration of the stock solution was compared with that of the diluted solution.
In your case, you know that the stock solution had a concentration of
This means that your solution was diluted by a factor of
#"D.F." = (11.0 color(red)(cancel(color(black)("M"))))/(0.100color(red)(cancel(color(black)("M")))) = 110#
If the concentration of the stock solution was
#color(purple)(|bar(ul(color(white)(a/a)color(black)("D.F." = V_2/V_1 implies V_2 = "D.F." xx V_1)color(white)(a/a)|)))#
In your case, you'll have
#V_2 = 110 * "2.50 mL" = color(green)(|bar(ul(color(white)(a/a)"275 mL"color(white)(a/a)|)))#
So, to prepare this solution, you'd start with

