Question

How do I us the Limit definition of derivative on `f(x)=e^x`?

Answer 1

The limit definition of the derivative is:

`d/dx f(x) = lim_(h->0) (f(x+h) - f(x))/h`

Now, since our function `f(x) = e^x`, we will substitute:

`d/dx[e^x] = lim_(h->0) (e^(x+h) - e^x)/h`

At first, it may be unclear as to how we will evaluate this limit. We will first rewrite it a bit, using a basic exponent law:

`d/dx[e^x] = lim_(h->0) (e^(x) * e^h - e^x)/h`

And now, we will factor the `e^x`:

`d/dx[e^x] = lim_(h->0) (e^x (e^h - 1))/h`

It might not be obvious, but using the constant law of limits we can actually treat `e^x` as a constant here and pull it out of the limit as a multiplier:

`d/dx[e^x] = e^x * lim_(h->0) (e^h - 1)/h`

And now, the entire thing has been simplified a great deal. The tricky part is figuring out this last limit.

Since it's easier, we will attempt to evaluate the limit graphically. So let's take a look at a graph of the function `y = (e^x - 1)/x` and see what happens when `x->0`:


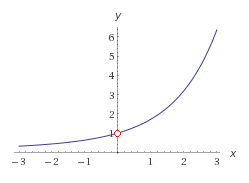
The "hole" at `x = 0` is caused by a division by zero. Thus, the function is undefined at `x = 0`. However, the function is well-defined everywhere else, even at values extremely close to zero. And, when `x` gets extremely close to zero, we can see that `y` appears to be getting closer to `1`:

`(e^0.1 - 1)/0.1 approx 1.0517`

`(e^0.01 - 1)/0.01 approx 1.0050`

`(e^0.001 - 1)/0.001 approx 1.0005`

And, we can observe this same trend when approaching from the negative side:

`(e^-0.1 - 1)/-0.1 approx 0.9516`

`(e^-0.01 - 1)/-0.01 approx 0.9950`

`(e^-0.001 - 1)/-0.001 approx 0.9995`

So, we can say with reasonable certainty that `lim_(h->0) (e^h - 1)/h = 1`.

Granted, one shouldn't assume that they will get the correct answer from evaluating a limit graphically. So, since I like certainty, and since there is a way to evaluate the above limit algebraically, I will explain the alternate method:

`lim_(h->0) (e^h - 1)/h`

Now, there are actually a few ways to define `e` itself as a limit. One of them is

`e = lim_(h->0) (1 + h)^(1/h)`

Since our previous limit also has the variable `h` approaching zero, we can actually substitute the definition of `e`.

`lim_(h->0) (((1 + h)^(1/h))^h - 1)/h`

Simplifying the inside gives:

`lim_(h->0) (1 + h - 1)/h`

This further simplifies to:

`lim_(h->0) h/h`

We can easily see that this limit evaluates to `1`.

So now that we know what this limit is, we can look back at our definition for the derivative of `e^x`.

`d/dx[e^x] = e^x * lim_(h->0) (e^h - 1)/h`

`= e^x * 1`
`= e^x`