How do you write the standard form of the equation of the circle with the given the center (0,0), r=12?

Question

3652 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-19T02:08:12

$x^{2} + y^{2} = 12^{2}$ $x^2 + y^2 = 12^2$

For a circle centered at $(a, b)$ $(a,b)$ with radius $r$ $r$ , the equation of the circle is given by

${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ $(x-a)^2 + (y-b)^2 = r^2$

This follows from the Pythagoras Theorem. Refer to the diagram below.

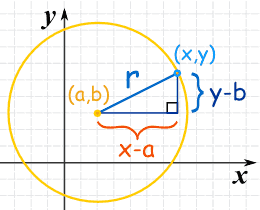
www.mathsisfun.com

In this case, $(a, b) = (0, 0)$ $(a,b) = (0,0)$ and $r = 12$ $r = 12$ . Therefore, the equation of the circle is

${(x - 0)}^{2} + {(y - 0)}^{2} = 12^{2}$ $(x-0)^2 + (y-0)^2 = 12^2$

or after simplifying,

$x^{2} + y^{2} = 144$ $x^2 + y^2 = 144$