What is the area enclosed by $r = - θ sin (- 16 θ^{2} + \frac{7 π}{12})$ $r=-thetasin(-16theta^2+(7pi)/12)$ between $θ \in [0, \frac{π}{4}]$ $theta in [0,(pi)/4]$ ?

Question

What is the area enclosed by $r = - θ sin (- 16 θ^{2} + \frac{7 π}{12})$ $r=-thetasin(-16theta^2+(7pi)/12)$ between $θ \in [0, \frac{π}{4}]$ $theta in [0,(pi)/4]$ ?

1 Answer

Impact of this question

2495 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-18T05:03:08

$A_{Total} = 0.0597217$ $A_"Total" = 0.0597217$

Explanation:

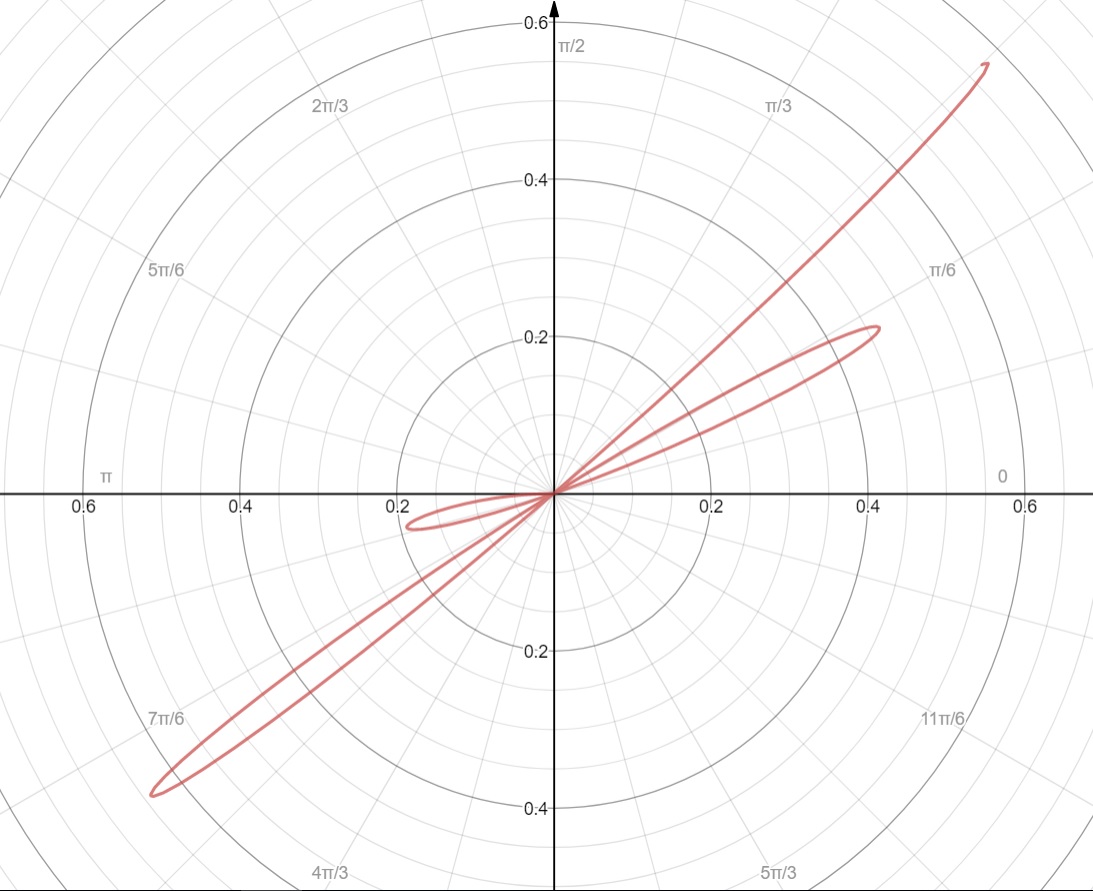
To determine an area in polar coordinates, it first helps to look at the graph that is depicted by the given parameters:

$r = - θ sin (- 16 θ^{2} + \frac{7 π}{12})$ $r=-thetasin(-16theta^2+(7pi)/12)$ with $θ \in [0, \frac{π}{4}]$ $theta in [0, pi/4]$

![Desmos.com and MS Paint]( useruploads.socratic.org )

Not every bit of the graph in within $[0, \frac{π}{4}]$ $[0,pi/4]$ is an enclosed area or loop. Once we find the $r$ $r$ and $θ$ $theta$ values corresponding to the three loops, we can use them as limits of integration. Each area formed by a loop can be determined by the formula:

$A = \int_{a}^{b} \frac{1}{2} f {[θ]}^{2} d θ$ $A=int_a^b1/2f[theta]^2 d theta$

Three loops, means three integrals. The roots of radius, $r$ $r$ , will give us the limits of integration.

$- θ sin (- 16 θ^{2} + \frac{7 π}{12}) = 0$ $-thetasin(-16theta^2+(7pi)/12) = 0$

The trivial solution is when $θ = 0$ $theta=0$ . Because the sine function is zero at $π n$ $pi n$ , we can say $sin (- 16 θ^{2} + \frac{7 π}{12}) = 0$ $sin(-16 theta^2 +(7pi)/12)=0$ whenever

$- 16 θ^{2} + \frac{7 π}{12} = π n$ $-16 theta^2 + (7pi)/12 = pi n$

$- 16 θ^{2} = π n - \frac{7 π}{12}$ $-16 theta^2 = pi n - (7pi)/12$

$θ^{2} = - \frac{π n}{16} + \frac{7 π}{192}$ $theta^2 = -(pi n)/16 + (7 pi)/192$

$θ = \pm \sqrt{- \frac{π n}{16} + \frac{7 π}{192}}$ $theta = +-sqrt(-(pi n)/16 + (7 pi)/192)$

We know $θ$ $theta$ is restricted to the interval $[0, π / 4]$ $[0, pi//4]$ . Because our interval involves only positive values, then we can write:

$0 \leq \sqrt{- \frac{π n}{16} + \frac{7 π}{192}} \leq \frac{π}{4}$ $0 <= sqrt(-(pi n)/16 + (7 pi)/192) <= pi/4$

$0 \leq - \frac{π n}{16} + \frac{7 π}{192} \leq \frac{π^{2}}{16}$ $0 <= -(pi n)/16 + (7 pi)/192 <= pi^2/16$

$0 \leq - π n + \frac{7 π}{12} \leq π^{2}$ $0 <= -pi n + (7 pi)/12 <= pi^2$

$- \frac{7 π}{12} \leq - π n \leq π^{2} - \frac{7 π}{12}$ $-(7 pi)/12 <= -pi n <= pi^2 - (7 pi)/12$

$\frac{7}{12} \geq n \geq - π + \frac{7}{12}$ $7/12 >= n >= -pi + 7/12$

$- 2.55826 \leq n \leq 0.583333$ $-2.55826 <= n <= 0.583333$

The integers, $n$ $n$ , that lie on this interval are $- 2, - 1, 0$ $-2, -1, 0$ . The respective angles, $θ$ $theta$ , with those values of $n$ $n$ are $θ = 0$ $theta=0$ and:

$θ \approx 0.3384, 0.5576, 0.7122$ $theta ~~0.3384, 0.5576, 0.7122$

Now we have our limits of integration for three integrals.

$A_{1} = \int_{0}^{0.3384} \frac{1}{2} {[- θ sin (- 16 θ^{2} + \frac{7 π}{12})]}^{2} d θ$ $A_1=int_0^0.3384 1/2[-thetasin(-16theta^2+(7pi)/12)]^2 d theta$

$A_{2} = \int_{0.3384}^{0.5576} \frac{1}{2} {[- θ sin (- 16 θ^{2} + \frac{7 π}{12})]}^{2} d θ$ $A_2=int_0.3384^0.5576 1/2[-thetasin(-16theta^2+(7pi)/12)]^2 d theta$

$A_{3} = \int_{0.5576}^{0.7122} \frac{1}{2} {[- θ sin (- 16 θ^{2} + \frac{7 π}{12})]}^{2} d θ$ $A_3=int_0.5576^0.7122 1/2[-thetasin(-16theta^2+(7pi)/12)]^2 d theta$

Using a computer algebra system, we get

$A_{1} = 0.0057972$ $A_1 = 0.0057972$

$A_{2} = 0.0225589$ $A_2 = 0.0225589$

$A_{3} = 0.0313656$ $A_3 = 0.0313656$

$A_{Total} = 0.0597217$ $A_"Total" = 0.0597217$

Science

Math

Humanities

... and beyond

What is the area enclosed by $r = - θ sin (- 16 θ^{2} + \frac{7 π}{12})$ $r=-thetasin(-16theta^2+(7pi)/12)$ between $θ \in [0, \frac{π}{4}]$ $theta in [0,(pi)/4]$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

What is the area enclosed by r=-thetasin(-16theta^2+(7pi)/12) r=−θsin(−16θ2+7π12)r=-thetasin(-16theta^2+(7pi)/12) between theta in [0,(pi)/4]θ∈[0,π4]theta in [0,(pi)/4]?

1 Answer

Explanation:

Related questions

Impact of this question

What is the area enclosed by $r = - θ sin (- 16 θ^{2} + \frac{7 π}{12})$ $r=-thetasin(-16theta^2+(7pi)/12)$ between $θ \in [0, \frac{π}{4}]$ $theta in [0,(pi)/4]$ ?