Question

A triangle has corners at points A, B, and C. Side AB has a length of `44`. The distance between the intersection of point A's angle bisector with side BC and point B is `16`. If side AC has a length of `32`, what is the length of side BC?

Answer 1

≈ 27.64

Explanation:

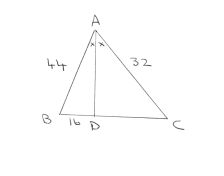The first step is to let the point where the angle bisector intersects with BC be D.

Then by the `color(blue)" Angle bisector theorem "`

`(BD)/(DC) = (AB)/(AC)`

Require to find DC.

Substitute the appropriate values into the ratio to obtain.

`16/(DC) = 44/32`

Now cross-multiply

`rArr 44xxDC = 32xx16`

now divide both sides by 44

`(cancel(44) DC)/cancel(44) = (32xx16)/44`

`rArr DC ≈ 11.64`

and BC = BD + DC = 16 + 11-64 = 27.64